概述
解析函式的一類冪級數展開式。在圓|z-α|<R內解析的函式ƒ(z)可以展為以下形式的冪級數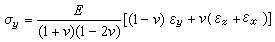 (1)
(1)
設z是圓│
 -α│<R內的任意一點,作圓γ;|
-α│<R內的任意一點,作圓γ;| -α|=r<R使得z位於γ的內部。根據柯西公式得到
-α|=r<R使得z位於γ的內部。根據柯西公式得到  (2)
(2)
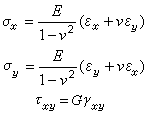 ,
,
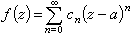 , (3)
, (3)
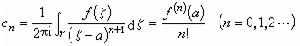 。 (4)
。 (4)
定理
根據解析函式可以展為泰勒級數 的上述事實,可以得到解析函式以下兩個重要性質。① 零點的孤立性 若ƒ(z)是域D內不恆為零的解析函式,則ƒ(z)在D內的零點是孤立的。也就是說,若ƒ(α)=0 (α∈D),則存在α的一個鄰域,使得ƒ(z)在該鄰域內除α點外沒有其他零點。② 惟一性定理 設ƒ1(z),ƒ2(z)是域D內的兩個解析函式,若存在點集A嶅D,它有一個屬於D的極限點α,且在A上ƒ1(z)=ƒ2(z),則在D內ƒ1(z)=ƒ2(z)。惟一性定理可由零點孤立性推出。
柯西不等式 若函式 ƒ(z)在圓│z-α│<R內是解析的,且│ƒ(z)│≤M,則ƒ(z)在圓│z-α│<R內的泰勒級數
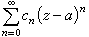 的係數сn滿足不等式
的係數сn滿足不等式 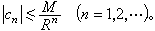 (5)
(5)
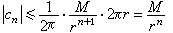 ,
,
劉維爾定理 若ƒ(z)是有窮複平面上的有界解析函式,則ƒ(z)必為常數。
事實上,這時(3)式在圓|z-α|<R內成立,R是任意正數,由柯西不等式立即推出сn=0(n≥1)即ƒ(z)呏с0(常數)。
作用
 常見的麥克勞林級數
常見的麥克勞林級數冪級數的求導和積分可以逐項進行,因此求和函式相對比較容易。
一個解析函式可被延伸為一個定義在複平面上的一個開區域上的泰勒級數通過解析延拓得到的函式,並使得複分析這種手法可行。
泰勒級數可以用來近似計算函式的值。
對於一些無窮可微函式f(x)雖然它們的展開式收斂,但是並不等於f(x)。例如,分段函式,當x≠0且f(0)=0,則當x=0所有的導數都為零,所以這個f(x)的泰勒級數為零,且其收斂半徑為無窮大,雖然這個函式f僅在x=0處為零。而這個問題在複變函數內並不成立,因為當z沿虛軸趨於零時並不趨於零。泰勒級數
一些函式無法被展開為泰勒級數是因為那裡存在一些奇點。但是如果變數x是負指數冪的話,我們仍然可以將其展開為一個級數。例如,就可以被展開為一個洛朗級數。
基本原理:多項式的k重不可約因式是其微商的k-1重不可約因式;
基本思想:通過係數為微商的多項式來研究任意函式的性質。
發展簡史
 Brook Taylor
Brook Taylor進入14世紀,MādhavaofSañgamāgrama最早使用了泰勒級數以及相關的方法。雖然沒有保留他的工作記錄,但後來印度數學家的著作表明他發現了一些特殊的泰勒級數,這些級數包括正弦,餘弦,正切,和反正切三角函式等等。之後,喀拉拉邦的天文與數學學校在他的基礎上進行了一系列的延伸與合理逼近,一直持續到16世紀。
到了17世紀,詹姆斯格雷戈(JamesGregory)同樣繼續著這方面的研究並且發表了若干麥克勞林級數。沒到1715年,布魯克泰勒(BrookTaylor)提出了一個常用的方法來構建這一系列級數並適用於所有函式。這就是後來被人們所熟知的泰勒級數。麥克勞林級數是以愛丁堡大學教授麥克勞林級數來命名的。他在18世紀發表了泰勒級數的特例。

