簡介
魯歇定理是關於解析函式在區域內部的零點個數的定理,是輻角原理的一個推論。
 魯歇定理
魯歇定理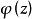 魯歇定理
魯歇定理設C是一條簡單閉曲線,函式 及 滿足條件:
(1)它們在C的內部均解析,且連線到C;
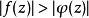 魯歇定理
魯歇定理(2)在C上, ,
 魯歇定理
魯歇定理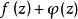 魯歇定理
魯歇定理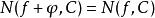 魯歇定理
魯歇定理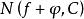 魯歇定理
魯歇定理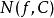 魯歇定理
魯歇定理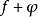 魯歇定理
魯歇定理 魯歇定理
魯歇定理則函式 與 在C的內部有同樣多(考慮階數)的零點,即 。這裡 和 分別表示 和在C內部的零點的個數。
舉例
 魯歇定理
魯歇定理方程 在單位圓內有5個根;
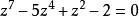 魯歇定理
魯歇定理方程 在單位圓內有4個根;
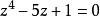 魯歇定理
魯歇定理方程 在單位圓內有1個根;
 魯歇定理
魯歇定理方程 在單位圓內無根。
輻角原理
幅角原理是關於解析函式在簡單閉曲線內部的零點個數與極點個數之間的關係的定理。
 魯歇定理
魯歇定理設Γ為一簡單閉曲線,函式 滿足條件:
 魯歇定理
魯歇定理1. 在Γ的內部除有有限個極點外是解析的;
 魯歇定理
魯歇定理2. 沿Γ上解析且不為零;
 魯歇定理
魯歇定理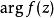 魯歇定理
魯歇定理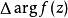 魯歇定理
魯歇定理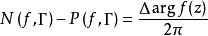 魯歇定理
魯歇定理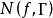 魯歇定理
魯歇定理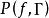 魯歇定理
魯歇定理則 在簡單閉曲線Γ內部的零點與極點個數之差,等於z沿Γ之正向繞行一周時, 的改變數 除以2π,即 ,這裡和分別表示在Γ內部的零點個數和極點個數。
