簡介
傳說在我國古代夏禹治水時,曾經看過洛水之中有一隻大烏龜,這隻烏龜的背上有幾個奇妙的花紋,引起了眾人的注目。仔細看這大龜身上的花紋,可以發現這花紋是由45個圓點所組成的,形成如左上圖的排列,後人便稱之為洛書。
我們可以利用阿拉伯數字來表示夏禹所發現的洛書,結果就可以看到如右圖的方陣。好奇的祖先們發現,這龜的圖形所代表的數字,不管是沿著橫行將數字一個一個加起來,或是沿著縱列,甚至於沿對角線計算數字和,都能夠得到數字和15這個奇妙的數字。
橫行各數字和: 4+9+2=15 3+5+7=15 8+1+6=15
縱列各數字和: 4+3+8=15 9+5+1=15 2+7+6=15
對角線數字和: 4+5+6=15 2+5+8=15
魔術方陣簡單的說,就是一個由1到n2 的數字所組成的n*n陣列,具有各對角線,各橫行與縱列的數字和都相等的性質。您不妨動手試試看,看看能不能在一個3x3或是4x4的方格陣列中造出魔術方陣來。當然,或許你能夠造出許多不同的魔術方陣,換言之,即3x3以上的方格陣列之魔術方陣個數不唯一。
歷史
根據「論說」和「星子」中的記載,傳說大約在三千年前, 夏禹治水時, 在洛水裡出現了一隻大烏龜, 龜背上刻有奇特的圖案,人們將他取名為洛書。
這個方陣具有一個奇特的性質,那就是每一行、每一列以及對角線上的數字和都是15。祖先們認為"洛書"是一個吉祥的象徵,所以許多人都將他畫在紙上攜帶,認為有保平安的效果。
在別的東方地區也有幻方的記載,但多數也蒙上神秘的色彩。較早期的一個,是刻在印度一所廟宇的石上,年代大約是十一世紀,是個4階幻方。古代印度的人民十分崇拜這種幻方,至今從古神殿的遺址、墓碑上常常還可以發現四階幻方的遺蹟,至今還有許多印度人把「洛書」的圖案佩在胸前當作護身符。
由於洛書共有九個數字,所以漢代的徐岳把他稱為九宮算 (或九宮圖) 。九宮算在漢代之後又有很大的擴展,成為縱橫均為n行的縱橫圖。而公元十世紀宋朝時,有人將「九宮」和「洛出書」合稱為「洛書」。
1275年,中國數學家揚揮在古摘奇算法中更進一步模仿洛書,計算出了五五幻方、六六幻方....九九幻方及百子幻方 (十階幻方) 等。後來程大位在1593年於算法統宗中繼承了揚輝的工作又作出十四個幻方,而張潮更將幻方推廣到正立方體上。
十二世紀的阿拉伯文獻里也有六階幻方的記載,我國考古學家曾經在西安也發現了五塊鐵板,上面刻有當時阿拉伯文獻上的五個六階幻方,也說明了我國與阿拉伯數學文化交流的情況。右圖即五個六階幻方中的一個。
直到西元13世紀時,東羅馬帝國的希臘數學家才對幻方產生興趣,但是成果不多。
在公元15世紀時,住在君士坦丁堡的魔索普拉把我國的縱橫圖介紹給歐洲人,並取名為magic square,因為縱橫圖具有如此變幻莫測的特別性質,所以在歐洲也掀起了一段占星的風潮,中古世紀的歐洲人也認為幻方具有符的法力,能夠鎮壓妖魔,許多歐洲寺院中的神殿都使用他,而許多占星術師也將其作為護身符。
別稱
魔術方陣是一種已流傳千年的數字陣列,不管是中西方對這奇妙的陣列都有所研究。
魔術方陣其實是由西方的"Magic square"翻譯過來的,當然,在東方也有不同的別稱。在中國我們稱之為幻方, 建構方法我國古代則有縱橫圖的稱呼。而日本則稱之為方陣。
建構方法
魔術方陣要滿足各行各列各對角線之和相等的條件,是否有簡單的方法可以達到這個目標呢? 以下我們就來探討一下有關魔術方陣建構的問題.
三階幻方的建構方法:
一開始我們由三階的魔術方陣做起,魔術方陣是一個有趣的數學問題,不過如果我們嚴肅的看他,其實魔術方陣就是一個滿足許多簡單數字和條件的一種方陣。假使我們將一個三階的魔術方陣用八個等式表現出來。
三階幻方建構:九子斜排,上下對異,左右相更,四維挺出, 戴九履一,左三右七,二四為肩,六八為足.
 魔術方陣 魔術方陣 |
三階幻方建構種類有8種,由幻方的旋轉,我們可以得到四種變化: 0度 90度 180度 270度 四種旋轉 若將幻方整個翻轉過來,又可以的到另外的四個不同的幻方,其他7個幻方: 原方陣 8 1 6 3 5 7 4 9 2 90度 4 3 8 9 5 1 2 7 6 180度 2 9 4 7 5 3 6 1 9 270度 6 7 2 1 5 9 9 3 4 鉛直 6 1 8 7 5 3 2 9 4 水平 4 9 2 3 5 7 8 1 6 左上右下 8 3 4 1 5 9 6 7 2 右上左下 2 7 6 9 5 1 4 3 8
四階幻方的建構方法
接下來我們來探討一下四階方陣的建構方法。首先我們觀察一下變數以及已之條件的變化情形。四階幻方的已之條件有10條(各行各列各對角線之和等於魔數),但是四階幻方的變數卻有16個之多。由此可知我們如果要利用像三階幻方那樣的"暴力"解法的話是行不通的。因此我們轉為利用分析的方式來一步一步的建構四階魔術方陣。
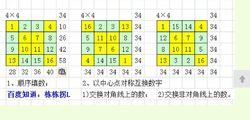
1、先把1放在四階幻方4個角的任意一個角格,按同一個方向按順序依次填寫其餘數。
如圖:按行從左向右順序排數。
2、以中心點對稱互換數字。(有兩種對稱交換的方法)
1)、以中心點對稱交換對角線上的數(即1-16、4-13、6-11、7-10互換),完成幻方,幻和值=34。
2)、以中心點對稱交換非對角線上的數(即2-15、3-14、5-12、8-9互換),完成幻方,幻和值=34。
 魔術方陣
魔術方陣高階幻方的建構方法
偶階幻方分兩類: 雙偶數:四階幻方,八階幻方,....,4K階幻方, 可用<對稱交換法>,方法很簡單:
1) 把自然數依次排成方陣
2) 把幻方劃成4*4的小區,每個小區劃對角線,
3) 把這些對角線所劃到的數,保持不動, 4) 把沒劃到的數,按幻方的中心,以中心對稱的方式,進行對調, 幻方完成!
單偶數:六階幻方,十階幻方,....,4K+2階幻方, 方法是很繁的,有一種稱<同心方陣法>:
1) 把幻方分成兩個區,一是框線一圈,二是裡面一個雙偶數方陣,
2) 把(3+8K)到(16K^2+8K+2)按雙偶數幻方方法填入雙偶數方陣,
3) 把餘下的數,在邊上試填,調整到符合為止.
1、奇數階魔術方陣時,最簡單: 把它叫做n階魔術方陣(n為奇數)
解法:⑴ 將1放在第一行中間一列;
⑵ 從2開始直到n×n止各數依次按下列規則存放:
按 45°方向行走,如向右上
每一個數存放的行比前一個數的行數減1,列數加1
⑶ 如果行列範圍超出矩陣範圍,則迴繞。
例如1在第1行,則2應放在最下一行,列數同樣加1;
⑷ 如果按上面規則確定的位置上已有數,或上一個數是第1行第n列時,
則把下一個數放在上一個數的下面。
例如:5階魔術方陣:
| 17 | 24 | 1 | 8 | 15 | |
| 23 | 5 | 7 | 14 | 16 | |
| 4 | 6 | 13 | 20 | 22 | |
| 10 | 12 | 19 | 21 | 3 | |
| 11 | 18 | 25 | 2 | 9 |

