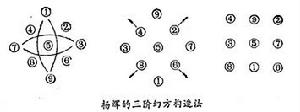
介紹
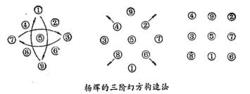 魔方矩陣
魔方矩陣在《射鵰》中郭黃二人被裘千仞追到黑龍潭,躲進瑛姑的小屋。瑛姑出了一道題:數字1~9填到三行三列的表格中,要求每行、每列、及兩條對角線上的和都相等。這道題難倒了瑛姑十幾年,被黃蓉一下子就答出來了。
4 9 2
3 5 7
8 1 6
這就是一個最簡單的3階平面魔方。因為魔方的智力性和趣味性,很多遊戲和玩具都與魔方有關,如捉放曹、我們平時玩的六面體,也成為學習編程時的常見問題。
歷史
魔方又稱幻方、縱橫圖、九宮圖,最早記錄於我國古代的洛書。據說夏禹治水時,河南洛陽附近的大河裡浮出了一隻烏龜,背上有一個很奇怪的圖形,古人認為是一種祥瑞,預示著洪水將被夏禹王徹底制服。後人稱之為"洛書"或"河圖",又叫河洛圖。
南宋數學家楊輝,在他著的《續古摘奇算法》里介紹了這種方法:只要將九個自然數按照從小到大的遞增次序斜排,然後把上、下兩數對調,左、右兩數也對調;最後再把中部四數各向外面挺出,幻方就出現了。 (摘自《趣味數學辭典》)
在西方,阿爾布雷特·丟勒於1514年創作的木雕《憂鬱》是最早關於魔方矩陣的記載。有學者認為,魔方矩陣和風靡一時的鍊金術有關。幾個世紀以來,魔方矩陣吸引了無數的學者和數學愛好者。班傑明·富蘭克林就做過有關魔方矩陣的實驗。
最簡單的魔方就是平面魔方,還有立體魔方、高次魔方等。對於立體魔方、高次魔方世界上很多數學家仍在研究。
每行、每列及對角線之和被稱為魔術常量或魔法總和,M。
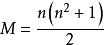 魔方矩陣
魔方矩陣其中,n為階數。
例如,如果n=3,則M=[3*(3^2+1)]/2 = 15.
魔方構造
平面魔方的一般定義:將自然數 1 到 N^2, 排列 N 行 N 列的方陣,使每行、每列及兩條主對角線上的 N 個數的和都等於N (N^2+1)/2,這樣的方陣稱為 N 階幻方。
通過搜尋整理後,得到下面的算法:
對平面魔方的構造,分為三種情況:N為奇數、N為4的倍數、N為其它偶數(4n+2的形式)
N 為奇數時
(1) 將1放在第一行中間一列;
(2) 從2開始直到n×n止各數依次按下列規則存放:
按 45°方向行走,如向右上
每一個數存放的行比前一個數的行數減1,列數加1
(3) 如果行列範圍超出矩陣範圍,則迴繞。
例如1在第1行,則2應放在最下一行,列數同樣減1;
(4) 如果按上面規則確定的位置上已有數,或上一個數是第1行第n列時,
則把下一個數放在上一個數的下面。
N為4的倍數時
採用對稱元素交換法。
首先把數1到n×n按從上至下,從左到右順序填入矩陣
然後將方陣的所有4×4子方陣中的兩對角線上的數關於大方陣中心作中心對稱交換(注意是各4×4子方陣對角線上的數), 即a(i,j)與a(n+1-i,n+1-j)交換,所有其它位置上的數不變。(或者將對角線不變,其它位置對稱交換也可)
N 為其它偶數時
當n為非4倍數的偶數(即4n+2形)時:首先把大方陣分解為4個奇數(2m+1階)子方陣。
按上述奇數階魔方給分解的4個子方陣對應賦值
上左子陣最小(i),下右子陣次小(i+v),下左子陣最大(i+3v),上右子陣次大(i+2v)
即4個子方陣對應元素相差v,其中v=n*n/4
四個子矩陣由小到大排列方式為 ① ③ ④ ②
然後作相應的元素交換:a(i,j)與a(i+u,j)在同一列做對應交換(j<t或j>n-t+2),
注意其中j可以取零。
a(t-1,0)與a(t+u-1,0);a(t-1,t-1)與a(t+u-1,t-1)兩對元素交換
其中u=n/2,t=(n+2)/4 上述交換使每行每列與兩對角線上元素之和相等。
算法設計
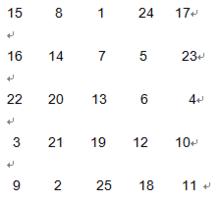 魔方矩陣
魔方矩陣先在矩陣第一行中間的位置上放1,然後把數字按照升序沿著左上角放置到矩陣中。如果越界了,就假設周圍還有一個矩陣,將數字放到那個位置上;如果那個位置已經被占據了,就跳過該位置放到下面的位置,然後重新按照原來的方法放。如圖:在5×5的魔術矩陣中,放完1以後,就把2放到1的左上角,但是此時已經越界了。假設,在原來的矩陣上面還有一個矩陣,則數字2所放的位置應該是在最後一行的第二個位置,接下去就要把數字3放到2的左上角,依次放下去,當放到6的時候,由於1已經將下一個位置占了,所以就放到5下面的位置。依照這樣的規律直到把數字都放完。
魔方函式
Matlab中自動生成魔方矩陣的函式:
magic(n) n是矩陣維數,例如在MATLAB命令視窗輸入
magic(5) ,將隨機產生5階魔方陣。