釋義
正文高聚物在外力作用下在應力-應變曲線上出現
 高聚物屈服
高聚物屈服相關知識屈服曲面qufuqum一an屈服曲面(yield。urfaee)屈服函式(f(氏,)二0)在主應力空間表現出的幾何曲面圖形。如在主應力空間特雷斯卡(H.Tresca)屈服條件是一個無限長的正六稜柱面,而米澤斯(R.vonMises)屈服條件是一個無限長的圓柱面(見屈服條件)。若主應力空間中,任意一點的坐標(稱為應力點)位於屈服曲面上,則意味著該點是滿足屈服條件的,即該點開始進入塑性變形狀態。若應力點位於屈服曲面以內(f(氏,)<0),則意味著該點是處於彈性變形狀傑
屈服曲線 yieldlocus
屈服曲線
屈服曲線(yieldloeus)屈服曲面與二平面或其他特定平面‘如某一主平面)的交截線。也有人把它稱為屈服軌跡。在二平面內,屈服曲線有以下重要特性:(1)屈服曲線是一條包圍原點的封閉曲線;(2)屈服曲線與從原點引出的任意一條矢徑線必須也只能相交一次;(3〕屈服曲線對原點是外凸的;(4)屈服曲線對稱於三個主應力軸在二平面的投影線及各自的垂線,可見屈服曲線有六條對稱軸線。
屈服台階 yieldterrace
屈服台階
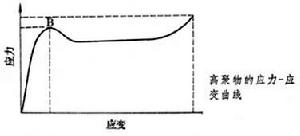
屈服台階(yieldterraee)在某些材料的拉伸曲線上與屈服伸長相對應的水平線段或曲折線段,又稱屈服平台。退火低碳鋼的拉伸曲線如圖所示。從圖上曲線看出,當載荷增加到一定數值時曲線突然下降,隨後在載荷不再增加或在某一不變載荷附近波動時,試樣會繼續產生伸長變形。載荷突然下降的點,稱為上屈服點(圖中A點);不變載荷或首次下降的最低載荷點,稱為下屈服點(圖中B點)。退火低碳鋼的拉伸曲線圖退火低碳鋼的屈服台階最為典型。屈服台階與位錯和溶質原子的相互作用有關。聚集在位錯周圍的碳、氮間隙原子使位錯被釘扎,使滑移困難,塑性變形開始時必須提高外力才能使位錯啟動,位錯一旦啟動後所需應力即迅速下降,位錯能在較低的應力作用下迅速揖移。形成屈服台階的機制與以下因素有關:材料在變形前可動位錯密度小(或雖有大量位錯,但多數被釘扎住);隨塑性變形的開始,位錯迅速增殖;位錯運動速率與外加應力。塑性變形的應變速率雲用下式表示:雲~b砰式中b為伯格斯矢量;p為可動位錯密度;下為位錯運動平均速率。位錯運動速率取決於應力的大小:獷一(r/ro)‘式中T為滑移面的切應力;r。為位錯以單位運動速率運動所需的切應力;冠為位錯運動速率的應力敏感係數。提高獷需較高的應力,得到較高的上屈服點,一旦塑性變形產生,由於位錯的增殖使位錯密度增加,相‘應的速率要下降,而對應的應力也會突然下降到下屈服點。體心立方點陣金屬的耐值較低(屏<20)具有明顯的屈服現象,面心立方點陣金屬的ml值較高(耐>100~200)故屈服現象不明顯。
屈服條件 yieldcondition
屈服條件
塑性力學中判斷物體處於彈性狀態還是處於塑性狀態的判據,是物體中一點在由彈性狀態轉變到塑性狀態時各應力分量的組合所應滿足的條件。
單向應力狀態的屈服條件由屈服極限(又稱屈服應力,見材料的力學性能)表示,可由實驗定出。對於屈服不明顯的材料,在工程中將殘餘應變為0.2%的應力值定義為條件屈服極限□□,或把拉伸曲線(圖1拉伸曲線)中割線模量□□=0.7□□處的應力作為條件屈服極限□□,其中□□為彈性模量。這種定義方法比測定殘餘應變數更簡便。對於一般鋼材,□□和□□很接近。某些金屬材料在外力作用下產生塑性變形,卸載後再載入,屈服應力會有所提高,這種現象稱為材料的強化現象。提高后的屈服應力稱為後繼屈服應力或載入應力。複雜應力狀態下的情形有所不同。
為了描述材料在複雜應力狀態下開始發生破壞時的受力程度,需要引入應力空間的概念,它是以應力分量為坐標的空間,在此空間中,每個點都代表一個應力狀態,應力的變化在相應的空間中給出一條曲線,稱為應力路徑。根據不同的應力路徑所進行的實驗,可以定出從彈性階段進入塑性階段的各個屈服應力。在應力空間中將這些屈服應力點連起來,就形成一個區分彈性區和塑性區的分界面,這個分界面稱為屈服面。描述屈服面的數學表達式就是屈服條件,它對應於單向應力狀態下的屈服極限。同單向應力狀態一樣,在經歷塑性變形後,低碳鋼等材料的屈服極限沒有什麼變化,而強化材料的後繼屈服應力比初始屈服應力有所提高。這些後繼屈服點連成的面稱為後繼屈服面或載入面。初始屈服面轉為後繼屈服面的變化規律稱為強化規律。
材料的初始屈服條件一般可表示為□(□□)=□,其中□□為應力分量;□為材料常數,可以通過實驗測定。對於各向同性材料,屈服條件可用三個主應力□□、□□、□□表示。這樣,屈服條件可簡化為□(□□,□□,□□)=□□。在以主應力為坐標軸的主應力空間中,同□對應的屈服面將空間分為兩部分:包含原點的屈服面內的部分對應彈性狀態(或剛性狀態);在屈服面上和屈服面外的部分對應塑性狀態。根據塑性力學的簡化假設,平均正應力□□=(□□+□□+□□)/3□不影響屈服,所以,□在主應力空間中是以□□=□□=□□的直線為軸的一個等截面柱體,截面的形狀可以在平面□□+□□+□□=0(稱為□□□平面)上決定。
法國的H.特雷斯卡於1864年通過許多擠壓實驗研究屈服條件。他發現被擠壓的金屬上有許多很細的痕紋,它們的方向接近於最大剪應力的方向。他認為當最大剪應力□□達到某一極限值□□(稱為剪下屈服極限)時,材料便進入屈服狀態。這一屈服條件稱為特雷斯卡條件或最大剪應力條件,其數學表達式為:
max(|□□-□□|,|□□-□□|,|□□-□□|)=2□□□。等式左邊表示取|□□-□□|、|□□-□□|、|□□-□□|中的最大者。等式在□□□平面上是一個正六邊形(圖2□□平面上的特雷斯卡條件和米澤斯條件)。
德國的R.von米澤斯於1913年提出,在□□□平面可用一個圓代替特雷斯卡的正六邊形(圖2□□平面上的特雷斯卡條件和米澤斯條件),相應的屈服條件稱為米澤斯條件,它避開了由於屈服面不光滑而帶來的數學上的困難。米澤斯屈服條件的表達式為:
後來,德國的H.亨奇提出,米澤斯屈服條件意味著在物體中的形變比能等於某一極限值時,材料就進入屈服狀態。因此,米澤斯屈服條件又稱為最大形變比能條件。
特雷斯卡屈服條件是一個線性的代數方程,知道主應力大小的次序後,使用這個條件比較方便;但在一般情況下事先並不知道主應力大小的次序,套用米澤斯屈服條件則比較方便,不過相應地要在數學上解一個非線性方程。
德國的W.洛德於1926年用薄壁管受拉伸和內壓聯合作用的試驗驗證屈服條件,他發現,對於碳素鋼和合金鋼等韌性材料,米澤斯屈服條件同試驗結果符合得較好。
各向異性材料的屈服條件一般比較複雜,表達式中包含有反映材料各向異性性質的特徵參量。