高斯光學
正文
又稱近軸光學,是幾何光學中研究共軸光學系統近軸區成像規律的一個分支。1841年德國科學家C.F.高斯在其著作中闡明了有關理論。基本概念 共軸光學系統 由透鏡、反射鏡等光學元件組成的系統,其中所有的折射面和反射面都是鏇轉對稱面,並有一個共同的對稱軸,稱為光軸。一般常見的共軸光學系統中折射面和反射面都是球面(平面當作半徑無窮大的球面看待),通過所有球面的球心的直線即光軸。
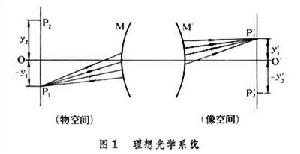
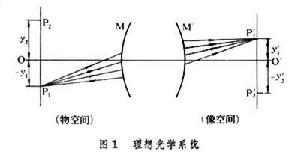
理想光學系統 能產生清晰的、與物體完全相似的像的光學系統。下面用圖1進一步說明。不討論光學系統的內部結構,只用最前表面M和最後表面M┡ 示意代表一個系統,OO┡為其光軸。物空間的一條光線經過光學系統中一系列光學表面的折射(或反射)後進入像空間,這條像空間光線和對應的物空間光線稱為一對共軛光線。由物點P1發出許多光線,如果系統是理想的,則像空間的所有共軛光線都通過同一點P姈。P姈是P1的清晰像點,它們互稱共軛點,通過P1的垂軸平面和通過P姈的垂軸平面是一對共軛面。P1和P姈到光軸的距離分別為物高y1和像高y姈;像高與物高之比,即β=y姈/y1稱垂軸放大率。在同一對共軛面上任意一對共軛點(如P2、P1)都有相同的垂軸放大率,因此理想光學系統所成的像與物有完全相似的幾何形狀。
 高斯光學
高斯光學高斯光學適用範圍 高斯光學的理論和公式適用於共軸光學系統的近軸區;當這個系統是理想光學系統時,對近軸區和非近軸區都同樣適用。通常遇到的系統雖然都不是真正的理想光學系統,但在光學設計過程中,各種像差都得到某種程度的校正,就一定的孔徑和視場範圍而言,系統接近於一個理想光學系統,因此高斯光學的計算結果(像的大小、成像位置等)對非近軸區也接近正確;當然,它與光線追跡結果或多或少有些差別,而這個差別正好能說明像差校正的完善程度。因此,高斯光學雖然只描述近軸區的成像性質,但在衡量非近軸區的成像狀況和質量方面是必不可少的。特別是在光學系統初步設計階段,高斯光學的理論和有關計算公式有其重要的實用意義。
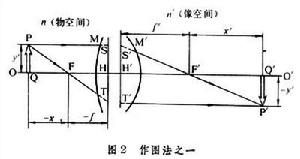
學科內容 焦點、主點和節點 共軸光學系統的幾個基點;過這些基點並垂直於光軸的平面,分別稱作焦面、主面和節面。像方焦點F┡是物空間無窮遠處光軸上物點的共軛點,凡是物空間中平行於光軸的光線都可認為來自無窮遠軸上物點,因而其共軛光線通過F┡(圖2)。與此類似,物方焦點F與像空間無窮遠軸上點共軛,從物方焦點發出的光線經系統後,必平行於光軸射出。物方主點H和像方主點H┡是一對共軛點,而兩個主面是共軛面,以垂軸放大率β=1為其特徵。例如S是物空間光線在物方主面上的交點,S┡是其共軛光線在像方主面上的交點,由於β=1,S和S┡這一對共軛點等高(即到光軸的距離相等)。同理,圖2中T和T┡也等高。
 高斯光學
高斯光學高斯光學的方便之處就在於處理成像問題時可以僅用基點和基面完全代替實際的光學系統。具體作圖方法如圖2所示,箭頭PQ代表物體,過P點作一條平行於光軸的光線,交物方主面於S,根據它的共軛光線通過F┡,以及S、S┡等高這兩個條件畫出共軛光線。另作一條通過P和物方焦點F的光線與物方主面交於T,根據它的共軛光線平行於光軸以及T、T┡等高這兩個條件畫出共軛光線。兩條共軛光線交於P┡,從而確定了PQ的像P┡Q┡的位置和大小。
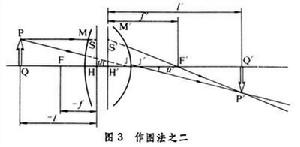
物方節點J和像方節點J┡也是一對共軛點,其特點是通過J的光線與通過J┡的共軛光線互相平行。根據節點的這一性質很容易用作圖方法求得物體的像(圖3)。
 高斯光學
高斯光學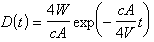 。 (1)
。 (1)
焦距和光焦度 物方焦距f是由H到F的距離(圖2);像方焦距f┡是由H┡到F┡的距離。焦點在主點之左時,焦距為負;反之,為正。圖2、圖3況,f<0,f┡>0 。光焦度的定義式為
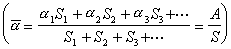 。 (2)
。 (2)
 高斯光學
高斯光學牛頓公式 一種描述物像關係的公式;可直接由圖2中相似三角形關係導出
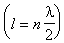 , (3)
, (3)
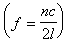 。 (4)
。 (4)
高斯公式 描述物像關係的另一種公式
 , (5)
, (5)
 , (6)
, (6)
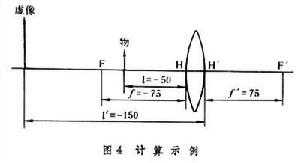
計算示例 對一個光學系統使用牛頓公式或高斯公式之前,必須求出其基點位置;通常用近軸光線追跡的辦法解決;但對某些簡單系統可利用一些現成公式。例如空氣中的透鏡,其材料折射率為n,兩個球面曲率半徑為R1和R2(球心在球面頂點右面時曲率半逕取正值),若透鏡厚度很小,可以忽略,則透鏡焦距可用下式計算
 。 (7)
。 (7)
如果用牛頓公式計算,則以x=l-f=25代入式(4)得x┡=-225(由F┡到虛像的距離),再用式(3)得β=3。