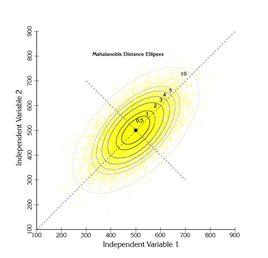
定義
馬氏距離也可以定義為兩個服從同一分布並且其協方差矩陣為Σ的隨機變數之間的差異程度。
如果協方差矩陣為單位矩陣,那么馬氏距離就簡化為歐氏距離,如果協方差矩陣為對角陣,則其也可稱為正規化的歐氏距離。
歐氏距離的缺點
我們熟悉的歐氏距離雖然很有用,但也有明顯的缺點。它將樣品的不同屬性(即各指標或各變數)之間的差別等同看待,這一點有時不能滿足實際要求。例如,在教育研究中,經常遇到對人的分析和判別,個體的不同屬性對於區分個體有著不同的重要性。因此,有時需要採用不同的距離函式。
馬氏距離與歐式距離的比較
馬氏與歐式距離的比較:
1)馬氏距離的計算是建立在總體樣本的基礎上的,這一點可以從上述協方差矩陣的解釋中可以得出,也就是說,如果拿同樣的兩個樣本,放入兩個不同的總體中,最後計算得出的兩個樣本間的馬氏距離通常是不相同的,除非這兩個總體的協方差矩陣碰巧相同;
2)在計算馬氏距離過程中,要求總體樣本數大於樣本的維數,否則得到的總體樣本協方差矩陣逆矩陣不存在,這種情況下,用歐氏距離計算即可。
3)還有一種情況,滿足了條件總體樣本數大於樣本的維數,但是協方差矩陣的逆矩陣仍然不存在,比如三個樣本點(3,4),(5,6)和(7,8),這種情況是因為這三個樣本在其所處的二維空間平面內共線。這種情況下,也採用歐氏距離計算。
4)在實際套用中“總體樣本數大於樣本的維數”這個條件是很容易滿足的,而所有樣本點出現3)中所描述的情況是很少出現的,所以在絕大多數情況下,馬氏距離是可以順利計算的,但是馬氏距離的計算是不穩定的,不穩定的來源是協方差矩陣,這也是馬氏距離與歐氏距離的最大差異之處。
馬氏距離的優劣:
優點:它不受量綱的影響,兩點之間的馬氏距離與原始數據的測量單位無關,由標準化數據和中心化數據(即原始數據與均值之差)計算出的二點之間的馬氏距離相同。馬氏距離還可以排除變數之間的相關性的干擾。
缺點:它的缺點是誇大了變化微小的變數的作用。
如果用dij表示第i個樣品和第j個樣品之間的距離,那么對一切i,j和k,dij應該滿足如下四個條件:
①若且唯若i=j時,dij=0
②dij>0
③dij=dji(對稱性)
④dij≤dik+dkj(三角不等式)
顯然,歐氏距離滿足以上四個條件。滿足以上條件的函式有多種,本節將要用到的馬氏距離也是其中的一種。
第i個樣品與第j個樣品的馬氏距離dij用下式計算:
dij =((x i 一x j)TS-1(x i一xj) )1/2(T、-1、1/2都是上標)
其中,T表示轉置,x i 和x j分別為第i個和第j個樣品的m個指標所組成的向量,S為樣本協方差矩陣。
馬氏距離在回歸分析中,是測量某一自變數的觀測量與同一自變數所有觀測量平均值差異的統計量,此值越大,說明該觀測量為影響點的可能性越大。
spss操作為:“分析”~“回歸”~“線性”~“統計”對話框~“殘差”欄~Mahalanobis距離