簡介
阿爾伯特·愛因斯坦在瑞士蘇黎世聯邦科技大學(Eidgenössische Technische Hochschule, ETH; Swiss Federal Institute of Technology)時期的數學老師赫爾曼·閔可夫斯基在愛因斯坦提出狹義相對論之後,於1907年將愛因斯坦與亨德里克·洛侖茲的理論結果重新表述成(3+1)維的時空,其中光速在各個慣性參考系皆為定值,這樣的時空即以其為名,稱為閔可夫斯基時空,或稱閔可夫斯基空間。
愛因斯坦一開始不認為這樣的表述有何重要性,但當他1907年開始轉往廣義相對論發展時,發現閔可夫斯基時空可說是其所要發展的理論架構的基礎,轉而對這樣的表述採取高的評價。
定義
 閔可夫斯基空間
閔可夫斯基空間 閔可夫斯基空間
閔可夫斯基空間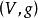 閔可夫斯基空間
閔可夫斯基空間設是實數域上的四維空間,若是一個非退化的對稱型且其正慣性指數等於3,則稱是一個閔可夫斯基空間。
 閔可夫斯基空間
閔可夫斯基空間在適當基下有如下矩陣:
 閔可夫斯基空間
閔可夫斯基空間 閔可夫斯基空間
閔可夫斯基空間 閔可夫斯基空間
閔可夫斯基空間 閔可夫斯基空間
閔可夫斯基空間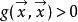 閔可夫斯基空間
閔可夫斯基空間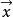 閔可夫斯基空間
閔可夫斯基空間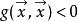 閔可夫斯基空間
閔可夫斯基空間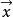 閔可夫斯基空間
閔可夫斯基空間上的正交變換即稱為洛倫茲變換,中的迷向向量稱為光向量,中適合的向量稱為空間向量,而適合的向量稱為時間向量.這些相關名詞指出了閔可夫斯基空間的物理學淵源。
推導
我們從空間坐標變換說起。我們知道,平面解析幾何中的坐標變換式是:
藉助矩陣的形式,我們可以把上式寫成:
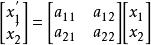 閔可夫斯基空間
閔可夫斯基空間這裡的變換矩陣
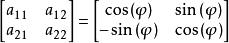 閔可夫斯基空間
閔可夫斯基空間是一個正交矩陣,因此這樣的坐標變換能保證任意兩點間距離不變。
 閔可夫斯基空間
閔可夫斯基空間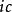 閔可夫斯基空間
閔可夫斯基空間 閔可夫斯基空間
閔可夫斯基空間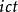 閔可夫斯基空間
閔可夫斯基空間從這裡只要一步就可以跨進狹義相對論。我們把時間 乘以一個因子 ,這裡 是具有速度量綱的一個常數,那么ict就有了長度的量綱(不過它的數值是虛的)。這個 就作為與三維空間的三個坐標相併列的第四維度,並且規定在坐標變換(實際上就是從一個慣性系變換到另一個慣性系)時,變換矩陣必須是正交的。比如,我們常見的洛侖茲變換:
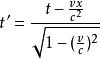 閔可夫斯基空間
閔可夫斯基空間 閔可夫斯基空間
閔可夫斯基空間 閔可夫斯基空間
閔可夫斯基空間 閔可夫斯基空間
閔可夫斯基空間 閔可夫斯基空間
閔可夫斯基空間 閔可夫斯基空間
閔可夫斯基空間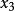 閔可夫斯基空間
閔可夫斯基空間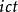 閔可夫斯基空間
閔可夫斯基空間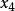 閔可夫斯基空間
閔可夫斯基空間如果把 、 、 依次記為 、 、 ,又記 為 ,寫成矩陣的形式就是:
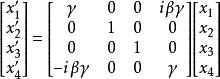 閔可夫斯基空間
閔可夫斯基空間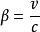 閔可夫斯基空間
閔可夫斯基空間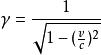 閔可夫斯基空間
閔可夫斯基空間上式中, , 。這么一來,“時空統一”看起來是不是清楚多了?
 閔可夫斯基空間
閔可夫斯基空間在這樣的正交變換之下,有一個叫做“四維間隔”的東西是守恆的。如果記間隔為 ,那么
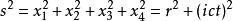 閔可夫斯基空間
閔可夫斯基空間 閔可夫斯基空間
閔可夫斯基空間 閔可夫斯基空間
閔可夫斯基空間這個“四維間隔”,也就是四維時空中兩點(準確地說應該叫做“時空點”)間的“距離”。上式最右邊的 是空間上的距離, 是時間上的距離。
 閔可夫斯基空間
閔可夫斯基空間與此同時, 就成了四維時空中一個非常獨特的速度。
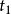 閔可夫斯基空間
閔可夫斯基空間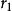 閔可夫斯基空間
閔可夫斯基空間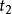 閔可夫斯基空間
閔可夫斯基空間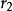 閔可夫斯基空間
閔可夫斯基空間假如:在某個慣性系S1看來,一個物體從A地勻速運動到B地,歷時 ,穿越距離 ;而在另一慣性系S2中,這一物體從A地到B地,歷時 ,穿越距離 ;那么在這兩個慣性系中,“物體從A地到B地”所經歷的“四維間隔”的平方分別是:
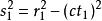 閔可夫斯基空間
閔可夫斯基空間和
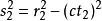 閔可夫斯基空間
閔可夫斯基空間 閔可夫斯基空間
閔可夫斯基空間 閔可夫斯基空間
閔可夫斯基空間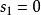 閔可夫斯基空間
閔可夫斯基空間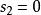 閔可夫斯基空間
閔可夫斯基空間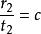 閔可夫斯基空間
閔可夫斯基空間 閔可夫斯基空間
閔可夫斯基空間 閔可夫斯基空間
閔可夫斯基空間 閔可夫斯基空間
閔可夫斯基空間 閔可夫斯基空間
閔可夫斯基空間 閔可夫斯基空間
閔可夫斯基空間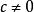 閔可夫斯基空間
閔可夫斯基空間倘若在S1系中此物體速度為 ,那么=c,於是 。則經過時空坐標的變換後必有 即 ,也就是說這一物體在S2系中的速度也是 。換句話說,只要時間 以一個固定的常數 (不管這是不是光速!)與空間相聯繫,那么以 為速度的物體在一切慣性系中的速度都是 。前提是 。
性質
可以證明閔可夫斯基空間的下列性質:
(1)任意兩個時間向量不可能相互正交;
(2)任意一個時間向量都不可能正交於一個光向量;
(3)兩個光向量正交的充分必要條件是它們線性相關。
閔可夫斯基空間的認識
閔可夫斯基世界是存在於一個虛構的四維時空中。所謂四維時空,和四維空間有區別。最明顯的區別是,四維時空中有一維是“類空間”,而四維空間的四個維都是空間。明確地講,四維空間中的四個維,可以視為具有相同性質的,而四維時空的類空間維,和其他三維不具有相同性質。所謂性質相同,其實包含很多方面,不很容易一下都總結出來,但是可以舉幾個常見例子:
(1)例如:在任何一維空間中度量空間長度的方法都是一樣的,這就是因為它們性質相同但我們很明顯地知道,在類空間中度量“類空間長度”的方法,是和在其他三維空間中度量長度的方法完全不同的。閔氏空間中的類空間維,準確來說就是 ict這一維,從取值來說,這一維上面的坐標或長度的取值是 0 或者純虛數,而其他三維空間中的坐標或長度取值一定都是實數。
(2)再比如:一個平面三角形在平直的四維空間中可以任意轉動,而且無論怎么轉,都能保持它作為三角形的標誌性幾何性質,且這些性質不隨時間或者這個四維平直空間變化,但這個三角形在四維時空中的轉動,一定只能是三維的,類空間這一維是不允許這個三角形介入的,如果強制這個三角形介入類空間一維,那么這個三角形就不是原來的三角形了,因為它的幾何性質中包含了隨時間改變的要素,這也會影響這個三角形在三維空間中的“剩餘部分”的幾何性質隨之變化。
因此,四維時空中的“長度”(準確說應該叫做“間隔”),並不是四維空間的長度概念,“間隔”這個概念本身就表明了物體的空間性質與時間性質的相關性,所以相對論中的物體運動的時間坐標和空間坐標是互相影響的,牛頓理論就沒有這個性質(牛頓理論的時間坐標不受空間坐標影響,只有空間坐標受時間坐標影響)。時空間隔不變性對應的是“相對性原理”。在牛頓理論的時空模型中,三維空間距離是參考系不變數,無論在哪個參考系下測量同一物體的長度得到的結果都是相同的,這是伽利略變換下的相對性原理的體現。相對論中,無論哪個參考系測量倆事件的四維時空間隔,也都得到相同的結果:四維時空間隔是不變數。
洛倫茲變換保證了“四維時空間隔”在參考系變換下擁有不變。洛倫茲變換是兩個參考系之間的變換關係。通常兩個參考系指的是運動速度不同的兩個參考系,但在四維時空的角度來看,這兩個參考系之間並不存在相對運動,而不過是兩者各坐標軸都擁有一個相同的固定的偏轉角度,所以也稱洛倫茲變換是一種四維時空旋轉變換。這種旋轉並不是三維空間中的那種旋轉,而是嵌入到時間維中一種“四維旋轉”。表現在三維空間中就是有相對運動速度。四維時空間隔是一個標量,標量在坐標變換中肯定是不變的。
從數學角度來說,四維時空間隔不變,體現的是閔氏時空的一種性質,這種性質很類似歐氏空間的性質:幾何不變性。而這種性質,往物理方面考慮,其實就是相對性原理的一種體現。閔氏時空其實不算是歐氏空間的直接推廣,因為它的第四維(時間維)與另外三個維的性質是有很大區別的。不過在數學或者幾何上,兩者有很多的共同之處,比如對距離的定義等等。閔氏時空有一個類別名稱叫做“偽歐氏空間”,這個“偽”字指出了它其實不是四維歐氏空間。四維間隔我們缺乏直觀的體驗,是因為我們(觀測者)在觀測的同時也在時間維中以固定的固有流逝速率“前進”,所以無法直接把握這個既包含空間距離也包含時間距離的思維間隔 。