內容概要:
均勻流體球自轉時的一種平衡形狀。1742年馬克勞林第一次嚴格證明:旋轉橢球體可以是均勻流體自轉時的平衡形狀。後來很多數學家改進了這項工作,成為天體形狀理論中第一個經典結論。若σ 為流體密度、ω為它的自轉速率、G 為萬有引力常數,則當參數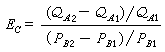

馬克勞林橢球體,均勻流體球自轉時的一種平衡形狀,成為天體形狀理論中第一個經典結論。
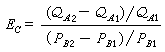
雅可比橢球體是均勻流體球自轉時的一種平衡形狀。1834年,雅可比證明:三軸橢球體(橢球體的三個軸彼此不相等)可以為均勻流體自轉時的平衡形狀。條件是參數Ω...
正文 作者介紹: 配圖 相關連線平衡形狀的穩定性理論。當Ω值較大時(仍小於1),相應的馬克勞林橢球體或雅...克勞林橢球體(旋轉橢球體)、雅可比橢球體(三軸不相等的橢球體)、龐加萊體...而言的,它們是橢球體或接近橢球體。有人證明,環狀體也可能成為平衡形狀,但不...
天體的形狀和自轉理論 正文 配圖 相關連線理由足以說明他是橢圓函式論的奠基人.在他之前,C.麥克勞林...人物簡介勒讓德出身於一個富裕家庭,就讀於巴黎的馬扎林(Maza-rin...9月18日生於巴黎 ,1833 年1月10日卒於同地。1770 年畢業於馬...
人物簡介 人物生平 主要貢獻 肖像爭議理由足以說明他是橢圓函式論的奠基人.在他之前,C.麥克勞林...人物簡介勒讓德出身於一個富裕家庭,就讀於巴黎的馬扎林(Maza-rin...9月18日生於巴黎 ,1833 年1月10日卒於同地。1770 年畢業於馬...
人物簡介 人物生平 主要貢獻 肖像爭議形狀分態①梨狀體或卵狀體。和雅可比橢球體相比,一頭稍大,另一頭稍小;②帶狀體。垂直於自轉軸的截面都是橢圓或圓,而子午截面不是橢圓,但與橢圓相差很小。與橢圓比較時,有的弧段上要凸出些,有的則凹下些;③扇狀體。它的子午...
形狀分態 研究經過。C.馬克勞林、P.-S.拉普拉斯和J.-L.拉格朗日等曾得到這樣的結論:當均勻流體取旋轉橢球體的形狀且繞旋轉軸轉動時,形狀不會改變。雅可比進一步發現:即使流體形狀是一般的橢球體,也滿足平衡條件。他深入研究了哈密爾頓...
人物生平 主要成就 雅可比行列式 雅可比矩陣