雅可比橢球體

雅可比橢球體是均勻流體球自轉時的一種平衡形狀。1834年，雅可比證明：三軸橢球體（橢球體的三個軸彼此不相等）可以為均勻流體自轉時的平衡形狀。條件是參數Ω （見馬克勞林橢球體）滿足下列條件﹕< =0.18711…。

正文

作者介紹：

雅可比（Jacobi,CarlGustavJacob）,德國數學家。1804年12月10日生於普魯士的波茨坦；1851年2月18日卒於柏林。

內容：

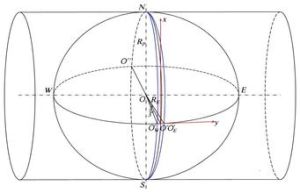
若a﹑b為橢球體赤道截面橢圓的半長徑和半短徑﹑c為橢球體的極半徑（在自轉軸上）﹐則a>c﹑b>c。這表明平衡形狀只能是扁球體。對小於的任一Ω值﹐都相應地存在一個三軸橢球體(a>b>c)的平衡形狀﹐稱為雅可比橢球體。在極限情況=時﹐a=b﹐相應的雅可比橢球體就成為馬克勞林橢球體。雅可比橢球體的赤道橢圓可以很扁﹐這在太陽系內的較大天體中尚未發現﹐但在星系中﹐如棒旋星系可能屬於這種類型。李亞普諾夫等人證明﹐雅可比橢球體是穩定的平衡形狀。

配圖

相關連線