定義
{a.b}[a.b]的意義
{a.b}是指a.b的小數部分;[a.b]指a.b的整數部分,a.b={a.b}+[a.b]
若a.b ≧0,則{a.b}=0.b,[a.b]=a
若a.b ≦0,則{a.b}=1-0.b,[a.b]=a-1
性質
| b>0 | b<0 | |
| 定義域 | x∈(-∞,+∞) | |
| 值域 | y∈[0,b) | |
| 增減性 | 在[kb,(k+1)b)增 | 在[kb,(k+1)b)減 |
| 過定點 | (0,0) | |
| 奇偶性 | f(-x)=b-f(x)是非奇非偶函式 | |
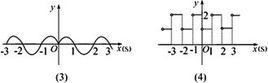
| 圖像 | 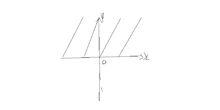 函式圖像 函式圖像 |  函式圖像1 函式圖像1 |
| 組成 | fe(x)=x-eb | fe(x)=eb-x |
| 周期 | T=b | |
方程與不等式
直接
xmoda=c
x=ka+c(k∈ Z)
xmoda>c
ka+c<x<(k+1)a(k∈ Z)
xmoda<c
ka<x<ka+c(k∈ Z)
間接
1、axmodb+c=0
設xmodb=y轉化成ay+c=0求解。
2、axmodb+cxmodb+d=0
設xmodb=y轉化成ay+cy+d=0求解。
3.
∑e=1a1ex1modb =c1
∑e=1xa2ex2 modb=c2
……
∑e=1anexnmodb=cn
設xemodb=ye轉化成
∑e=1a1e y1=c1
∑e=1a2ey2 =c2
……
∑e=1aneyn=cn
求解。
4.
∑e=1a1exmodb1 =c1
∑e=1xa2exmodb2 =c2
……
∑e=1anexmodbn=cn
設xmodbe=ye轉化成
∑e=1a1e y1=c1
∑e=1a2ey2 =c2
……
∑e=1aneyn=cn
求解。
求得
ye=c'e時
得x=k[be]+[ce ](則[be]是be的最低公倍數。)
運算
公式
(x+y)modb=(xmodb+ymodb)modb
(xy)modb =(xmodbymodb)modb
(/y)modb=(/ymodb)modb
(x)modb=(xmodb)modb
y=A(wx+v)modb+z(A>0,v>0)
圖像:先把 y=xmodb的圖像向左(v>0)或向右(v<0)平移/v/個單位,再把所得的點的橫坐標縮短(w>1)或伸長(0<w<1)到原來的1 / w個單位長度,再把所得的點的縱坐標縮短(A>1)或伸長(0<A<1)到原來的1 / A個單位長度,向上(z>0)或向下(z<0)平移/z/個單位。
微積分
y=xmodb不可導;
∫xmodb=/2x+c
套用區域
(1)星期,b=7
(2)時間,b=24,12
(3)三角函式,b=360°∪180°
(4)循環的東西
例題
方程與不等式
例1:解方程:xmod4=0
解:x=4k(k∈ Z)
例2:解不等式:4xmodb +3xmodb+3<0
解:a=4>0,又△=9-3×4=-3<0,原不等式的解集是☉。
運算
例:計算1/xmod3(x>1)
解:=x^-1mod3
=(xmod3)^-1
套用
例1:今天是星期二,再過12天是星期幾?
=(2+12)mod7=14mod7-=0
再過12天是星期日。
例2:今天是11月12日,再過30天是幾月幾日?
=(12+30)mod30=12
再過30天12月12日
例3:會議23:30開始,開了2h,幾時結束?
=(23.5+2)mod24=1.5
1:30結束