正式定義
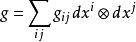 音樂同構
音樂同構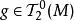 音樂同構
音樂同構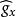 音樂同構
音樂同構黎曼流形M的黎曼度量 是一個二階的對稱、正定張量場 。在任意一點x∈M,黎曼度量會誘導出一個映射
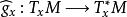 音樂同構
音樂同構 音樂同構
音樂同構這映射給了點 的切空間跟餘切空間之間的一個線性同構,對任何切向量X屬於TM,定義
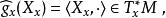 音樂同構
音樂同構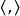 音樂同構
音樂同構其中符號 代表 流形上的黎曼度量。這意味著,
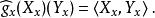 音樂同構
音樂同構這些線性映射的集合定義了一個叢同構
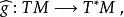 音樂同構
音樂同構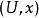 音樂同構
音樂同構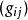 音樂同構
音樂同構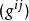 音樂同構
音樂同構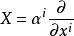 音樂同構
音樂同構 音樂同構
音樂同構這是一個特別的微分同胚,在每個切空間上為線性映射。在截面的層次上即是切向量場到餘切向量場的同構。在一個局部坐標 下,設度量矩陣為 ,逆矩陣為 ,向量場 。則這個同構會將 映射到
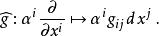 音樂同構
音樂同構這裡使用了愛因斯坦求和約定。
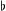 音樂同構
音樂同構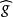 音樂同構
音樂同構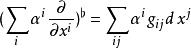 音樂同構
音樂同構 音樂同構
音樂同構以上同構稱為 降號音樂同構(flat)用符號 表示,例如以上的函式 可表示成: ;而其逆運算稱為 升號(sharp)用符號 表示:降號下降指標,升號上升指標,(Gallot,Hullin & Lafontaine 2004,p.75)。升號用局部坐標表示為:
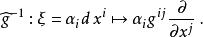 音樂同構
音樂同構這兩個同構的核心是g為處處非退化的雙線性形式,任何一個非退化的雙線性形式都可給出類似的同構,對偽黎曼流形、辛流形也有類似的同構。在辛幾何中,這個同構非常重要,哈密頓向量場便是由這個同構導出的。
名稱由來
 音樂同構
音樂同構 音樂同構
音樂同構 音樂同構
音樂同構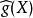 音樂同構
音樂同構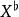 音樂同構
音樂同構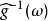 音樂同構
音樂同構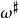 音樂同構
音樂同構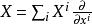 音樂同構
音樂同構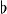 音樂同構
音樂同構同構 與其逆 稱為“音樂同構”是因為是因為常常用兩種音樂符號 來代替這些同構,比如 會寫成 , 會寫成 ,它們將指標向下、向上移動。例如,流形上的向量場 經過 映射會變成余向量場:
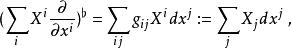 音樂同構
音樂同構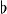 音樂同構
音樂同構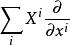 音樂同構
音樂同構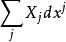 音樂同構
音樂同構 音樂同構
音樂同構這裡 將 映射到 ,係數的指標從上到下,所以這運算用降號符號 表示。
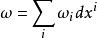 音樂同構
音樂同構 音樂同構
音樂同構而余向量 ,經過 運算會變成向量
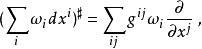 音樂同構
音樂同構 音樂同構
音樂同構 音樂同構
音樂同構所以指標向下、向上移動好似符號降號( )與升號( )下降與上升一個半音的音高
