概念
數學中， 里奇平坦流形（Ricci-flat manifold）是里奇張量為零的黎曼流形。在物理學中，它們代表了愛因斯坦方程在任何維數之黎曼流形且宇宙常數為零的類比，其所具有的真空解。里奇平坦流形是愛因斯坦流形的特殊情形，後者的宇宙常數並不需要為零。
里奇平坦流形在一般情形下，被限制屬於和樂群。其中重要的例子包括有卡拉比–丘流形與超凱勒流形。
黎曼流形
黎曼流形是一黎曼度量的微分流形。設M是n維光滑流形，若在M上給定一個光滑的二階協變張量場g，稱(M，g)為一個n維黎曼流形，g稱為該黎曼流形的基本張量或黎曼度量，如果滿足：
1.g是對稱的，即：
g(X，Y)=g(Y，X) (X，Y∈TM，p∈M).
2.g是正定的，即：
g(X，X)≥0 (X∈TM，p∈M)，
且等號僅在X=0時成立。
簡單地說，黎曼流形就是給定了一個光滑的對稱、正定的二階張量場的光滑流形。
微分流形
設M是仿緊豪斯道夫 (Hau-sdorff)空間，且是拓撲流形，稱A= {(U，Ф)|α∈P}是它的地圖，如果{U|α∈P}是M的開覆蓋，Ф是從U到n維歐氏空間R的某開集上的同胚。(U，Φ)稱為坐標卡。如果兩個坐標卡 (U，Ф)，(Uβ，Φ) 滿足U∩U≠Φ，則稱Φ·Ф：Φ(U∩U) →Φ(U∩U) 和Φ·Φ： Φβ(U∩U) →Ф(U∩U) 為U∩U上的坐標變換。如果A的所有坐標變換都是C可微的，則稱A為一個C地圖，其中1≤r≤∞。r也可等於ω，此時A稱為解析地圖。拓撲流形M的坐標卡 (U，Φ) 稱為與A是Cr相容的，如果任意(U，Φ) ∈A，坐標變換Φ·ΦΦ·Φ均C可微。拓撲流形M的C地圖A稱為最大的，如果它包含M的所有與之C相容的坐標卡。M上的最大C地圖A稱為M的C微分結構。(M，A)稱為C微分流形，或簡稱為C流形。當r=∞時，C微分結構也稱為光滑結構，C流形也稱為光滑流形。r=ω時，C結構也稱為解析結構，C流形稱為解析流形。C流形(M，A)有時也簡記為M。
從直觀上看，拓撲流形是局部歐氏空間，局部之間用同胚映射(坐標變換)貼上在一起。n維C流形，不僅局部同胚於n維歐氏空間，而且局部之間是用C光滑、且其逆也C光滑的坐標變換貼上在一起。
兩個C流形M和N，f：M→N是連續映射，且任一點P∈M，有包含P點的M中的坐標卡(U，Φ)以及包含f(P)的N中的坐標卡(V，∅)，使得f(U)⊂V，同時，映射∅°f°Φ：Φ(U)→∅(V)是C光滑的(1≤r≤∞或r=ω)，則稱f是C映射。C映射也稱為光滑映射，C映射也稱為解析映射。其中稱為f的局部表示。
里奇張量
里奇張量是黎曼流形的一個重要二階對稱張量。設(M，g)是一個黎曼流形，R(·，·，·，·)是它的曲率張量。對於X，Y∈Γ(TM)，若：
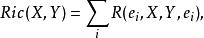里奇平坦流形其中{e}稱為M上的局部標準正交標架場，則Ric在每一點p∈M給出了TM×TM上的多線性函式，即它是一個(0，2)型張量場，稱為里奇張量.里奇張量是對稱的，即Ric(X，Y)=Ric(Y，X)。在局部坐標系(U;x)下，記：
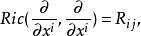里奇平坦流形則：
里奇平坦流形