判定定理
定理1
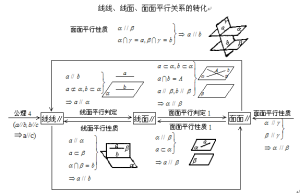 面面平行
面面平行已知α⊥l,β⊥l。求證α∥β
證明:假設它們不平行,那么它們相交,設交線為m。
設l與α的垂足為A,與β的垂足為B,在m上任意取一點P,連線PA、PB。
∵l⊥α,AP⊂α
∴l⊥AP
同理,l⊥BP
由於P和l構成一個平面,在這個新的平面上經過P就有兩條直線AP、BP與l垂直,與垂直定理矛盾。
∴假設不成立,α∥β
推論
如果兩個平面的垂線平行,那么這兩個平面平行。(可理解為法向量平行的平面平行)
證明:由線面垂直的性質可知兩條平行線與兩個平面都垂直,運用定理1可知面面平行。
定理1及其推論是向量法證明面面平行的基礎,如果兩個平面的法向量平行或相等,那么這兩個平面平行。
定理2
如果一個平面內有兩條相交直線與另一個平面平行,那么這兩個平面平行。
幾何語言:a⊂α,b⊂α,且a∩b=A,a∥β,b∥β。則α∥β。
反證法證明:假設這兩個平面不平行,那么它們相交,設交線為l。
∵a∥β
∴a與β無交點
同理,b與β無交點
∵l是兩個平面的交線,l⊂β
∴a與l無交點,b與l無交點,那么它們平行或異面。
又∵a⊂α,b⊂α,l⊂α,即它們不異面
∴a∥l,b∥l
∴a∥b
這與已知條件a∩b=A矛盾,因此假設不成立,α∥β
向量法證明:設直線a,b的方向向量為a,b,平面β的法向量為p。
∵a∥β,b∥β
∴a⊥p,b⊥p,即a·p=0,b·p=0
∵a,b是α內兩條相交直線
∴設有任一向量c⊂α,根據平面向量基本定理可知,存在一對有序數對(x,y)使得c=xa+yb
那么p·c=p·(xa+yb)=xp·a+yp·b=0
即p⊥c
由c的任意性可知p與α內任一向量都垂直,即p也是α的法向量。
∴α∥β
定理3
如果一個平面內有兩條相交直線分別與另一個平面內的兩條相交直線平行,那么這兩個平面平行。
幾何語言:a⊂α,b⊂α,且a∩b=A。c⊂β,d⊂β,且c∩d=B。a∥c,b∥d,則α∥β
證明:過A作直線l⊥β,先討論垂足不是B的情況。設垂足為C,過C作m∥c、n∥d。
∵a∥c,m∥c
∴a∥m
由於兩條平行直線確定一個平面,l在a與m確定的平面上(因為l經過A和C,而A∈a,C∈m):
∵l⊥m
∴l⊥a
同理l⊥b
∵a∩b=A,a⊂α,b⊂α
∴l⊥α
∵l⊥β
∴α∥β(定理1)
當l與β的垂足是B時,則無需經過垂足作c、d的平行線這一步,後面證法完全相同。
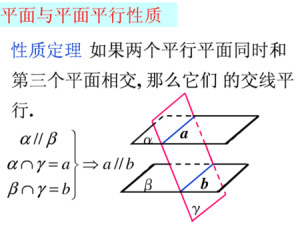
性質定理
定理1
兩個平面平行,在一個平面內的任意一條直線平行於另外一個平面。證明:設α∥β,a⊂α,則a∥β
∵α∥β
∴α與β無交點
又∵a⊂α
∴a與β無交點
即a∥β
定理2
兩個平行平面,分別和第三個平面相交,交線平行。如果交線不平行的話,設交線交點為P,那么P屬於兩條交線,即P屬於兩個平行平面,這是不可能的事情。所以交線必定平行。
定理3
兩個平面平行,和一個平面垂直的直線必垂直於另外一個平面。(判定定理1的逆定理)已知:α∥β,l⊥α。求證:l⊥β
證明:先證明l與β有交點。若l∥β
∵l⊥α
∴α⊥β(面面垂直的判定),與α∥β矛盾,因此l與β一定有交點。
設l∩α=A,l∩β=B
在α內,過A任意作一條直線a,那么a∩l=A
因此a與l確定一個平面。明顯,由於l與β是相交的,因此這個被a和l確定的平面也與β是相交的。
設與β的交線為b,由定理2可知a∥b
∵l⊥α,a⊂α
∴l⊥a
∴l⊥b
再經過A在α內任意作與a不重合的直線c,過l和c的平面與β相交於d,則同理可證l⊥d
明顯b和d是相交的,這是因為假設b∥d,由於a∥b,c∥d,可推出a∥c,但a和c都是經過點A作出來的,這樣就產生了矛盾
∵l與β內相交直線b、d都垂直
∴l⊥β
推論
兩個平行平面的垂線平行或重合。
證明:重合的情況很容易證,平行的情況可以根據定理3先判定一條直線與兩個平面都垂直,然後根據線面垂直的性質得到兩條直線平行。
定理4
三個平行平面截兩條直線,形成的對應線段成比例。已知:α∥β∥γ,直線m分別與三個平面相交於A、B、C,直線n分別與三個平面相交於D、E、F。
求證:AB:BC=DE:EF
證明:連線AD、CF、AF,設AF∩β=O,連線BO、EO
∵α∥β,平面ADEO截α和β的交線分別為AD、EO
∴AD∥EO(定理2)
在△ADF中,∵AD∥EO
∴AO:OF=DE:EF
同理,在△AFC中,有AO:OF=AB:BC
∴AB:BC=DE:EF
推論
經過三角形一邊作一個平面(與三角形所在平面不重合),與此平面平行的平面截三角形另外兩邊(或延長線)所得的線段對應成比例。
定理5
平行平面間的距離處處相等。已知:α∥β,AB⊥α,DC⊥α,且A、D∈α,B、C∈β
求證:AB=CD
證明:連線AD、BC
由線面垂直的性質定理可知AB∥CD,那么AB和CD構成了平面ABCD
∵平面ABCD∩α=AD,平面ABCD∩β=BC,且α∥β
∴AD∥BC(定理2)
∴四邊形ABCD是平行四邊形
∴AB=CD
定理6
經過平面外一點,有且只有一個平面與已知平面平行。已知:P是平面α外一點
求證:過P有且只有一個平面β∥α
證明:
先證明存在性。在α內任意作兩條相交直線a、b,過P分別作a'∥a,b‘∥b,則a’和b‘確定一個平面β。由判定定理3可知β∥α
再證明唯一性。假設過P有兩個平面β1、β2都與α平行,則過P作l⊥α,根據性質定理3,l⊥β1且l⊥β2。
再根據判定定理1,β1∥β2,這就和β1和β2同時經過點P矛盾。
兩個以上的情況證明類似,所以過P有且只有一個平面β∥α。