基本介紹
定義
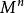 非退化臨界點
非退化臨界點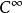 非退化臨界點
非退化臨界點 非退化臨界點
非退化臨界點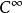 非退化臨界點
非退化臨界點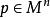 非退化臨界點
非退化臨界點 非退化臨界點
非退化臨界點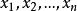 非退化臨界點
非退化臨界點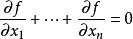 非退化臨界點
非退化臨界點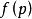 非退化臨界點
非退化臨界點 非退化臨界點
非退化臨界點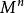 非退化臨界點
非退化臨界點 非退化臨界點
非退化臨界點 非退化臨界點
非退化臨界點設是類流形,是類函式。點稱為函式的臨界點,如果在局部坐標下,等式成立。數稱為函式的 臨界值,流形上所有其餘的點將稱為函式的 非臨界點,所有不是函式臨界值的數稱為這個函式的 非臨界值。
 非退化臨界點
非退化臨界點臨界點稱為 孤立的,如果可找到它的這種鄰域,在其中沒有其它的臨界點。臨界點稱為 非退化的,如果二階偏導數的矩陣是非退化的;反之,臨界點稱為 退化的。
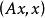 非退化臨界點
非退化臨界點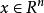 非退化臨界點
非退化臨界點 非退化臨界點
非退化臨界點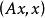 非退化臨界點
非退化臨界點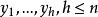 非退化臨界點
非退化臨界點考慮二次型,其中,它稱為函式在點p處的Hessian二次型。因矩陣A是對稱的,二次型可通過適當地選取坐標,化為正則形式
 非退化臨界點
非退化臨界點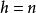 非退化臨界點
非退化臨界點如果A非退化,則。
 非退化臨界點
非退化臨界點 非退化臨界點
非退化臨界點 非退化臨界點
非退化臨界點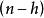 非退化臨界點
非退化臨界點 非退化臨界點
非退化臨界點數稱為函式在點的指標,而數稱為函式在點p的 退化度 。
例題解析
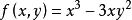 非退化臨界點
非退化臨界點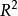 非退化臨界點
非退化臨界點由公式給定一個上的函式,顯然,偏導數
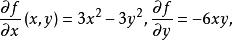 非退化臨界點
非退化臨界點 非退化臨界點
非退化臨界點 非退化臨界點
非退化臨界點它們僅在點同時為零。因此點是孤立臨界點,所有的二階偏導數
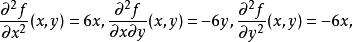 非退化臨界點
非退化臨界點 非退化臨界點
非退化臨界點 非退化臨界點
非退化臨界點 非退化臨界點
非退化臨界點 非退化臨界點
非退化臨界點 非退化臨界點
非退化臨界點 非退化臨界點
非退化臨界點 非退化臨界點
非退化臨界點 非退化臨界點
非退化臨界點在處也都為零,因此函式在點處的二階偏導數的矩陣是零矩陣,而函式在點的Hessian二次型恆等於零,這表明,臨界點是退化的,在點處,的退化度為2,指標為0 。
相關定理及概念
Morse引理
臨界點理論中的一個重要事實是:在臨界點的附近函式可表示為二次型的形狀,且函式的性態由它的指標來描述。
 非退化臨界點
非退化臨界點 非退化臨界點
非退化臨界點 非退化臨界點
非退化臨界點 非退化臨界點
非退化臨界點 非退化臨界點
非退化臨界點定理1(Morse引理) 設是函式的非退化臨界點,則在點的某鄰域U中存在這樣的局部坐標系,使得,並且在U上成立以下恆等式
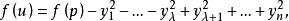 非退化臨界點
非退化臨界點 非退化臨界點
非退化臨界點 非退化臨界點
非退化臨界點 非退化臨界點
非退化臨界點 非退化臨界點
非退化臨界點其中是點的坐標,而是函式在點p的指標。
梯度場
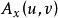 非退化臨界點
非退化臨界點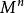 非退化臨界點
非退化臨界點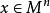 非退化臨界點
非退化臨界點 非退化臨界點
非退化臨界點 非退化臨界點
非退化臨界點設是上的Riemann度量,對每一點,選一個向量,使得以下條件成立:對任意的向量,成立等式
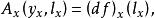 非退化臨界點
非退化臨界點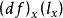 非退化臨界點
非退化臨界點 非退化臨界點
非退化臨界點 非退化臨界點
非退化臨界點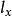 非退化臨界點
非退化臨界點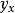 非退化臨界點
非退化臨界點 非退化臨界點
非退化臨界點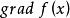 非退化臨界點
非退化臨界點其中是函式在點的微分在向量處的值。所得的場稱為函式的梯度場,記作。

