簡介
但在有些情況下，觀測值不遵從常態分配，而遵從其他類型的分布，比如偏態分布。
相對常態分配而言，將不遵從常態分配的其他類型的分布統稱為非常態分配。
論述
1、在實際遇到的許多隨機現象都服從或近似服從常態分配 。當樣本頻率分布直方圖就無限接近於一條總體密度曲線，總體密度曲線較科學地反映了總體分布。但總體密度曲線的相關知識較為抽象，學生不易理解，因此在總體分布研究中我們選擇常態分配作為研究的突破口。常態分配在統計學中是最基本、最重要的一種分布。
2．常態分配是可以用函式形式來表述的。其密度函式可寫成：
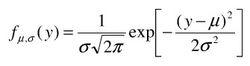常態分配密度函式，（σ>0，-∞<x<+∞）
由此可見，常態分配是由它的平均數μ和標準差σ唯一決定的。常把它記為。
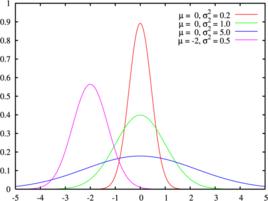
3．從形態上看，常態分配是一條單峰、對稱呈鐘形的曲線，其對稱軸為x=μ，並在x=μ時取最大值。從x=μ點開始，曲線向正負兩個方向遞減延伸，不斷逼近x軸，但永不與x軸相交，因此說曲線在正負兩個方向都是以x軸為漸近線的。
4．通過三組常態分配的曲線，可知正態曲線具有兩頭低、中間高、左右對稱的基本特徵。
5．由於常態分配是由其平均數μ和標準差σ唯一決定的，因此從某種意義上說，常態分配就有好多好多，這給我們深入研究帶來一定的困難。但我們也發現，許多常態分配中，重點研究N（0，1），其他的常態分配都可以通過轉化為N（0，1），我們把N（0，1）稱為標準常態分配，其密度函式為，x∈（-∞，+∞），從而使常態分配的研究得以簡化。
6．結合正態曲線的圖形特徵，歸納正態曲線的性質。正態曲線的作圖較難，教科書沒做要求，授課時可以藉助幾何畫板作圖，學生只要了解大致的情形就行了，關鍵是能通過正態曲線，引導學生歸納其性質。
