簡介
電阻網路比擬:用離散的電阻器組成的網路代替上述導電介質,同樣可以模擬拉普拉斯方程和泊松方程所描述的現象。
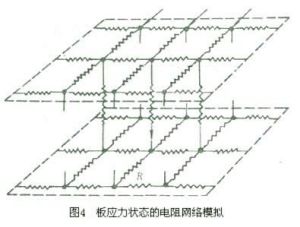
此外,還可設計出表示各種彈性結構的應力或應變的電阻網路。板應力狀態的電阻網路模擬所示的電阻網路,為互相聯接的雙層網路,相鄰的每兩個節點之間的電阻都為□,從某一或某些節點通入電流,則各電阻都有一定的電流分布,使每兩節點之間有一定的電壓分布,因而可模擬雙調和方程所描述的力學問題。例如板在其自身平面內受載時,其應力狀態可由下列雙調和方程描述:
 電阻網路比擬
電阻網路比擬式中φ(□,□)為艾里應力函式。如在上層網路的內節點輸入電流,即可模擬板在橫向受載時的問題:
式中□(□,□)為板的橫向撓度函式;□為單位面積載荷;
式中□為板的厚度;□為泊松比。
電阻網路法還可用來模擬梁和桁架的斜率-撓度方程,以及用來研究架構中的風載和沉陷應力、梁和板的振動和瞬態應力。
比擬法
analogymethod
是實驗應力分析方法的一種。它是根據兩種物理現象之間的比擬關係,通過一種物理現象的觀測試驗,研究另一種物理現象的方法。如果兩種(或兩種以上)物理現象中有可用形式相同的數學方程描述的物理量,它們之間便存在比擬關係,比擬法即因此得名。此法的優點是,用一種較易觀測試驗的物理現象,模擬另一種難以觀測試驗的物理現象,可使試驗工作大為簡化。在實驗應力分析領域中,常用的有薄膜比擬、電比擬、電阻網路比擬和沙堆比擬等方法。
薄膜比擬
從彈性理論得知,均勻張緊的彈性薄膜的橫向撓曲和等截面受扭直桿的橫截面中的剪應力,都由泊松方程描述:
□其邊界條件分別為:
□式中□為薄膜的撓度;□為單位面積上的橫向力;為薄膜邊界上單位長度內的拉力;□為扭轉應力函式;□為剪下模量;□為單位長度的扭轉角(弧度);為薄膜和桿件的橫截面的邊界(□=1,2);□、□為直角坐標。由此可見,如薄膜的邊界在一個水平面上,其形狀和受扭桿件的橫截面相似,而且C□/□□=2□□(□為比例常數),則撓度□(□,□)和扭轉應力函式□(□,□)成比例。試驗時,在一塊平板上開一個和受扭桿件的橫截面形狀相似的孔,將薄膜(如橡皮膜、肥皂膜等)張在孔上,然後在薄膜的一側微微施加氣壓,使它撓曲。測繪出薄膜撓曲後的等高線(圖1薄膜比擬)。由等高線圖可得出如下結果:①薄膜上任意點的等高線的切線方向,就是受扭桿件橫截面上的對應點的剪應力方向。②薄膜上任意點的最大斜率(可由等高線的豎直和水平間距算出)和受扭桿件橫截面上對應點的剪應力大小成比例。若在同一平板上開一圓孔(如圖1薄膜比擬右邊的圓孔),張上相同的薄膜,並施加同樣的氣壓,就可以標定出這一比例值。③撓曲薄膜表面和平板表面之間所包含的體積和受扭桿件的扭矩成比例。
如果薄膜上的單位面積的橫向力□=0,則可模擬拉普拉斯方程描述的力學問題,即
□在平面應力場中,□=(□□+□□)表示主應力和,它和薄膜的高度□成比例。薄膜比擬特別適用於確定非圓截面桿件的扭轉性能。
電比擬
考察導電板(或電解槽)的一個單元□□□□,如流經該單元四周邊界的電流為□□,□□,□□,□□(圖2流經導電板□□□□單元的電流),則導電板內的電勢分布由拉普拉斯方程描述:
□。(7)
如按圖3在□□□□單元表面輸入恆定電流□□所示,在該單元表面再輸入另一電流I□,則式(7)右邊不再等於零,而等於-□I□,從而可用下述泊松方程描述:
□(8)式中□(□,□)為電勢分布函式;□為導電介質的電阻率;I□為外加電流。因此,只要使導電板(或電解槽)的邊界形狀和模擬物體的形狀保持相似,並在邊緣加上和已知邊界值成比例的電勢,就可用來模擬這兩個方程所描述的範圍很廣的各種力學問題。當然,在泊松方程的情況下,還須在導電板(或電解槽)的邊界內部輸入恆值電流(它相當於用薄膜比擬時所加的單位面積橫向載荷□)。
沙堆比擬
從塑性理論得知,理想塑性材料的等截面直桿受扭轉達到極限狀態時,其橫截面上的剪應力分布可用拋物型方程描述,即
□,(12)其邊界條件為:
□,(13)式中□(□,□)為應力函式;□□為剪下屈服極限;□為橫截面的邊界。
沙堆試驗的基本方程為:
□,(14)式中□為沙堆表面的高度;□為沙堆的梯度。因為式(12)和式(14)之間存在比擬關係,故可用沙堆來模擬這種全塑性扭轉的應力分布問題。這時,沙堆的梯度相當於□□;沙堆的高度分布□(□,□)相當於應力函式□(□,□)。根據應力函式與剪應力的關係式,以及(12)和(14)式的比擬關係,得:
□則直桿所受的扭矩為:
□(17)式中□為桿件的截面面積;□為沙堆的體積,其數值的兩倍和扭矩的數值相當。沙堆試驗是將一塊金屬板製成和受扭桿件的橫截面相似的形狀,平放在一個鐵框架的支座上,將沙子覆蓋在上面,用四根鐵絲繩將這鐵框架懸掛在水平的位置,然後將鐵框架緩慢地提起,堆在金屬板上的沙子便形成各種形狀的沙堆模型(圖5沙堆試驗)。
參考書目
W.Hendry,ElementsofExperimentalStressAnalysis,PergamonPress,Oxford,England,1977.
(蘇先基)
