電磁質量和輻射阻尼
正文
在帶電粒子所產生的電磁場中，有一部分是脫離粒子向外輻射的場,稱為輻射場,而另一部分則是依附於帶電粒子的場，稱為帶電粒子的自場（見運動帶電粒子的電磁場）。輻射場將帶走能量,使粒子能量逐漸衰減,因此,它必然會對粒子產生反作用。在經典電動力學中,這種反作用是通過輻射場對粒子的作用力來體現的。這種作用力即為輻射阻尼力。而依附於粒子的場(自場)，將使粒子獲得一個附加質量，這就是粒子的電磁質量。對於電磁質量這裡亦只作經典的討論。典型的自場是等速運動粒子的場（靜止粒子可作為它的一個特殊情況）。這時輻射場為零。粒子所產生的全部電磁場都屬於自場。
在粒子速度比光速 с小得多的情況(非相對論情況)，自場的動量和能量分別等於
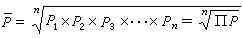
μ =4Uo/(3с2)。
當粒子速度改變時，不僅它自己的動量和能量要改變，依附於它的自場的動量和能量也將隨之改變。如果粒子原來的質量為 mo，則當粒子速度自v1改變到v2時，需要供給它的動量和能量就不僅僅是 mo（v2-v1）和
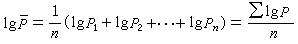，而應是(mo+μ)(v2-v1)和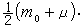
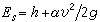。這表明，由於粒子攜帶著自場，它所表現出的慣性就比原來的大，相當於在原有質量mo之上再加一個質量μ。μ就是粒子的電磁質量。 實驗上所測量的帶電粒子的質量（稱為粒子的物理質量）其實並不是mo，而是mo+μ。這是因為帶電粒子總是同它的自場聯繫在一起，兩者不可分離，而原有質量（通常稱為裸質量）和電磁質量在物理效果上又是完全相同的緣故。
設帶電粒子是半徑為ro的球體,電荷q按體積均勻分布。這時
，
。
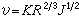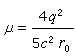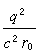，只是前面係數不同。由此可見,如果帶電粒子是一個嚴格的點（點模型），則粒子的物理質量將為無窮大，因而它將完全不能運動。這就是點模型的發散困難。 H.A.洛倫茲和M.阿伯拉罕曾提出這樣一種假設：電子的質量可能完全是電磁的，即mo=0，電子的慣性就是它的自場的慣性。這樣，在電荷按體積均勻分布的假設下，電子的物理質量m就將為
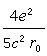，其中 e 表示電子的電荷。由此得出ro等於
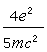。此結果中的係數
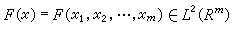並無重要意義，因其大小依賴於電荷分布的具體假設。但
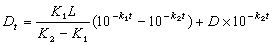卻具有典型的意義。它代表在洛倫茲-阿伯拉罕假設下，從經典理論計算出的電子半徑的一般量級。因此通常把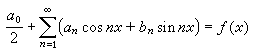 
ro=2.82×10-13cm。
需要注意，此值並不代表電子的真正大小，這不僅因為“電子的全部物理質量就等於它的電磁質量”本身只是一個假定，更重要的是，對於微觀物理問題，經典理論已不能適用。即使電子的電磁質量 μ在量級上與它的物理質量m相同，由於電子和電磁場服從量子規律,經典理論算出的半徑值也不可能在量級上是正確的。目前基本粒子物理方面的實驗資料,已經指明,電子半徑要比10-16厘米還要小。儘管如此，rc是一個由電子的一些基本參量（質量和電荷）和光速с（從相對論觀點看來,它是物理學中的一個基本常數）所組成的具有長度量綱的量。在許多公式中rc常作為一個特徵長度出現，因此仍然是有用的。輻射阻尼力可以通過能量守恆關係從帶電粒子的能量輻射率導出。對於低速運動的帶電粒子，輻射功率為
，
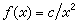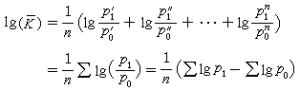
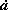代表加速度的時間變化率。 一般情況下，輻射阻尼力比電子所受到的外力要弱得多,只當在
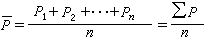這樣短促的時間內（rc即為上文中引入的電子經典半徑），加速度的改變數達到加速度本身的量級時，輻射阻尼力才與外力可以比擬。而這種條件是很少能滿足的。 在經典理論中，通常對原子採用諧振子模型。利用上述輻射阻尼力公式，可以研究諧振電子的阻尼振動。在此情況，輻射阻尼力與電子所受的外力(彈性恢復力)的比值約為
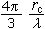，λ 代表振子輻射波的波長。對於原子發射的可見光來說，λ≈5×10-5cm,上述比值約為10-8的量級。就是對於波長為1┱的X 射線，比值也只有10-4的量級。這表明輻射阻尼確實是很小的。於是，可以用近似的方法來考慮輻射阻尼力的影響。這樣得出振子的振幅X隨時間衰減的關係為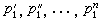 
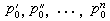代表振子的壽命。 振子的阻尼振動不是嚴格的周期振動，它所發射的電磁波也將不具有某一個嚴格的頻率，而具有一定的頻譜分布，即振子輻射場的譜線將具有一定寬度。對於原子譜線，導致譜線具有寬度的原因有多種，例如原子間的碰撞、都卜勒效應等。但這些因素與輻射過程無本質的聯繫，它們所造成的寬度也是可以設法削減的（例如降低發光氣體的密度和溫度）。只有輻射阻尼是能量守恆定律的要求，是自然存在的。因此通常把它所造成的寬度稱為譜線的自然寬度。用波長表示時，譜線自然寬度的值為
。
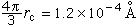以上求出的振子譜線的自然寬度值雖然是從經典理論推出來的，但在量子理論中，當躍遷是從諧振子第一激發態到基態時，求出的結果也與此相同。當然，實際的原子並非諧振子，故實際原子譜線的自然寬度與上述值有所不同。
參考書目
曹昌祺著:《電動力學》,人民教育出版社,北京,1961。
J.D.傑克遜著，朱培豫譯：《經典電動力學》，下冊，人民教育出版社,北京,1980。(J.D.Jackson,ClassicalElectrodynamics,John Wiley & Sons,New York,1976)
