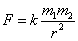簡介
電磁學量有多種單位制，它們之間的關係比較複雜，需要從單位制定的原則上加以說明。
單位制
物理學中確定單位制的通常作法是：選定某幾個物理量及其單位作為基本量和基本單位；其他物理量的量綱和單位則是從特定的物理公式通過選定其中比例常量得出來的，這樣得出的單位稱為導出單位。例如力學中的CGS單位制,就是取長度、質量和時間為基本量，它們的單位分別為厘米、克和秒，其他力學量的量綱和單位都由此導出。如力的量綱和單位是根據牛頓第二定律F＝kma並選定k＝1而得出的，其量綱為LMT，它的單位達因即為克·厘米／秒。
需要注意的是
① 如果選取不同的物理公式,則規定出的單位不僅大小可能不同，量綱也可能不一樣。例如若換用萬有引力定律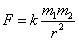 
並令其中的k=1來確定力的單位，則所得出的力的單位不僅大小與達因不同，連量綱也變為LM。若採用這一改變就從通常的 CGS單位制變到另一種不同的CGS單位制。
② 基本量的數目和選擇也不是惟一的。例如可以只取長度和質量為基本量，通過真空中光速с＝1來確定時間單位。這樣，時間的量綱就是長度，時空將具有一致的量綱。若長度單位仍取為厘米,那么“1厘米的時間”就代表真空中光走1厘米距離所花的時間,約等於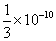 
秒。在粒子物理學中，常取
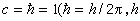為普朗克常數), 這樣定出的單位制叫做自然單位制,它只有一個基本量綱和單位。
由此可見，建立一種單位制，首先要選定基本量和基本單位，然後還要選定確定其他物理量單位的物理公式。
單位制的選用完全根據使用的方便。一般來說，基本量的數目選得多，有助於區別不同物理量的量綱，但物理公式較複雜，將有較多的物理常數出現；反之，公式比較簡單，但具有相同量綱的物理量的數目將增多。
電磁學中主要的單位制有五種
CGSE制
又稱靜電單位制(esu)。在此單位制中，基本量為長度、質量和時間。基本單位為厘米、克和秒。電荷的單位是通過庫侖定律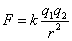 
並令k＝1確定的。這樣確定的電荷單位叫電荷的CGSE制單位(又稱靜庫侖)，電荷的量綱即為LMT。然後可從F＝qE、 
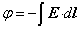、P＝ρl(ρ為電荷密度、l為位移)和D＝E＋4πP分別確定電場、 電勢、極化強度和電位移的 CGSE制單位。其中電勢單位又稱靜伏特。由此可以看出，在CGSE制中,P和D的量綱都與E的相同，因此極化率ⅹ，介電常數（電容率）ε都是無量綱的數。
電流密度和電流的單位分別通過j＝ρv和I＝jA（A為面積）或I=dq/dt來確定,這樣確定的電流單位又稱靜安培。
在CGSE制中，磁學量如H和B的單位是利用它們同電學量相互聯繫的物理公式確定的。這些物理公式可取為安培環路定理和法拉第電磁感應定律
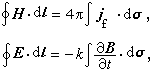
並令其中的比例常數k＝1。這樣確定的B和H具有不同的量綱。即使在真空中H也不等於B，而是H＝сB，с為真空中光速。因此在CGSE制中，磁導率μ是有量綱的,其量綱為LT；真空中磁導率
。
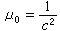總結起來，在 CGSE制中麥克斯韋方程組 的形式為
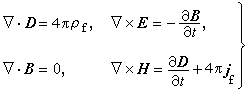(1)
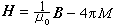而真空中洛倫茲力公式採取下列形式 
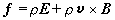; (2)
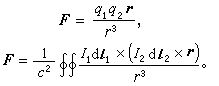
CGSM制
又稱電磁單位制(emu)。CGSM 制的基本量和基本單位與CGSM制的一樣，但是確定電磁量單位的物理公式不同。它是通過安培-畢奧-薩伐爾定律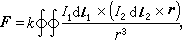
令k=1來確定電流的單位,再通過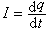
確定電荷單位。這樣確定的電荷單位與CGSE制中的量綱不同。
在電流和電荷的單位確定後,可以通過dF＝Idl×B、m＝IA（m為磁矩，A為面積）、H＝B-4πM、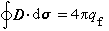
、 
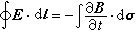來定義B、m、H、D和E的單位。在CGSM制中，B和H的單位相同，但通常B的單位稱為高斯，H的單位稱為奧斯特。磁導率μ是無量綱的。但E和D有不同的量綱，在真空中
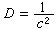E,因此介電常數ε量綱為LT,真空介電常數為ε0=1/c。
麥克斯韋方程組和洛倫茲力公式的形式與CGSE制中相同，即式(1)和式(2)。但庫侖定律和安培-畢奧-薩伐爾定律卻採取
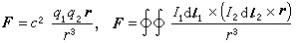
高斯單位制
在此單位制中，凡是電學量如q、I、E、P、D等都用CGSE制單位，而磁學量如E、M、H都用CGSM制單位。因而此在單位制中,介電常數ε和磁導率μ都是無量綱的，而且其真空值ε0＝μ0＝1。此外B和E的量綱相同。在高斯單位制中，凡是同時含有電學量和磁學量的公式都會出現常數 с。麥克斯韋方程組和真空中洛倫茲力公式分別為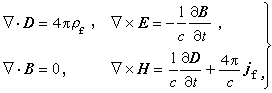
(3)
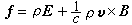。 (4)
庫侖定律、安培-畢奧-薩伐爾定律與CGSE制的相同。在理論物理中常採用這一單位制。
洛倫茲－亥維賽單位制 此單位制基本與高斯單位制相同，只是為了消去麥克斯韋方程組(3)中的4π 因子而略有變化。在此單位制中，凡“荷電物質”方面的量如q、I、P、M等，其單位都是高斯單位的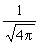 
，凡屬“場”方面的量如E、D、B、H等，其單位都是高斯單位的
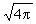倍。於是有
D＝E＋P，H＝B－M。
麥克斯韋方程組為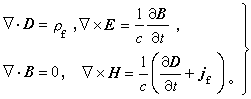
(5)
。
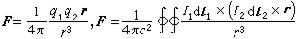國際單位制(SI)
此單位制的電磁學部分的基本量為長度、質量、時間和電流，基本單位分別為米、千克、秒和安培。1安培電流等於十分之一 CGSE制單位的電流。力、功和功率單位分別為牛［頓］、焦［耳］和瓦［特］。電荷、電場、電位單位可通過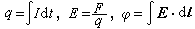
確定，並分別為庫、牛／庫（等於伏／米）和伏。電位移D的單位通過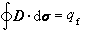
確定，它的量綱與E的不同，因而ε為有量綱的量,其真空值 
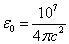庫/(千克·米）（其中c本身帶量綱）。
B和E的單位是通過法拉第電磁感應定律和安培環路定理確定的，即令
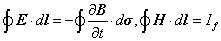
這樣確定的B和H的單位彼此不同，量綱也不同。磁導率的真空值為 μ0=4π×10千克·米/庫,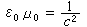
。麥克斯韋方程組為
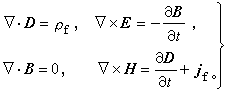(6)
。
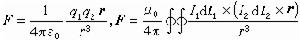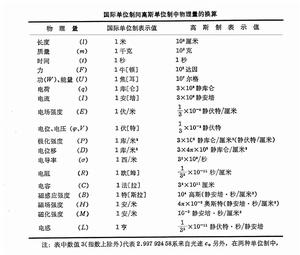
在電工和實用方面常採用這一單位制，並已作為實際計量單位在中國推廣套用。上表列出一定量的各種物理量在兩種單位制中的表示值。
