基本物理量
 自然單位制
自然單位制微觀物理學中涉及的基本物理量原有長度、時間、質量、電荷和溫度等五種,為了減少獨立的基本物理量的數目,利用庫侖定律並規定真空的介電常數為無量綱的數1或1/4π來定義電荷,從而使電荷不再是基本物理量。在粒子物理學中,考慮到所處理問題都屬於微觀高速運動範圍,利用三個普適常數來減少獨立的基本物理量的個數,從而把獨立的量綱減少到只有一種。
使用方法
自然單位制最常見的定義法是設定單位為1。例如,很多自然單位制會定義光速c = 1。假設速度 v 是光速的一半,則從方程 v = c / 2 與 c = 1 ,可以得到結果 v = 1 / 2。方程 v = 1 / 2 的意思為,採用自然單位制測量得到的速度 v 的數值為 1 / 2 ,或速度 v 是自然單位制的單位速度的一半。
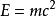 自然單位制
自然單位制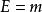 自然單位制
自然單位制方程 c = 1 可以帶入任意方程。例如,愛因斯坦方程 可以重寫為採用自然單位制的。這方程的意思為,粒子的靜能量,採用自然單位制的能量單位,等於粒子的靜質量,採用自然單位制的質量單位。
公式
kg,s,C,K→m:
G/c^2 [m/kg]
c [m/s]
((G/(4*π*(ε0)))^0.5)/c^2 [m/C]
(G*k)/c^4 [m/K]
m,s,C,K→kg:
c^2/G [kg/m]
c^3/G [kg/s]
1/(G*4*π*(ε0))^0.5 [kg/C]
k/c^2 [kg/K]
m,kg,C,K→s:
1/c [s/m]
G/c^3 [s/kg]
((G/(4*π*(ε0)))^0.5)/c^3 [s/C]
(G*k)/c^5 [s/K]
m,kg,s,K→C:
c^2/((G/(4*π*(ε0)))^0.5) [C/m]
(G*4*π*(ε0))^0.5 [C/kg]
c^3/((G/(4*π*(ε0)))^0.5) [C/s]
(k*(G*4*π*(ε0))^0.5)/c^2 [C/K]
m,kg,s,C→K:
c^4/(G*k) [K/m]
c^2/k [K/kg]
c^5/(G*k) [K/s]
c^2/(k*(G*4*π*(ε0))^0.5) [K/C]
常數
利用玻耳茲曼常數 k=(1.380662±0.000044) ×10-16erg/K=(8.61735±0.00028)×10-11 MeV/K,規定其值為無量綱的1,這樣溫度和能量將具有同一量綱,從而可以用同一單位來度量。這樣規定後,原有的溫度與能量單位的換算關係為:1eV=(11604.50±0.38)K。利用真空光速с=299792458×10^7m/s,規定其值為無量綱的1,這樣時間和長度將具有同一量綱,從而可以用同一單位來度量,這樣規定後,原有的時間和長度單位的換算關係為:1s=299792458×10^7m,利用普朗克常數h=(1.0545887±0.0000057)×10-27erg·s=6.62606896(33)×10^(-22)MeV·s,規定其值為無量綱的1,這樣時間和能量的倒數將具有同一量綱,從而可以用同一單位來度量。這樣規定後,原有的時間和能量單位之間的關係為:1MeV-1= (6.582173±0.000017)×10^(-22)s。
經過以上的規定,只剩下一種獨立的量綱,它可以選作能量、長度、時間,或其他任何一種有量綱的物理量。以這種物理量的單位作為基本單位導出其他物理量的單位,這就是自然單位制。
自然單位制中只有一種獨立的量綱,相應地只有一種基本單位,但並未統一規定取哪個單位為基本單位。在粒子物理學中,根據實際工作的需要,常選能量為基本量綱,選能量的單位MeV或GeV為基本單位。在這樣的選取下,質量也取MeV或GeV為單位,長度和時間都取MeV-1或GeV-1為單位,角動量為無量綱的量。有時根據需要也用fermi(10-131cm)作為長度的單位,它與能量單位之間的關係為:1fermi=(5.0676896±0.0000131)GeV-1。
精細結構常數 α=1/(137.03604±0.00011)在自然單位制中的表達式對應於兩種定義電荷的方式分別為α=e2/4π和α=e2,即在自然單位制中為無量綱的量。
優點和缺點
與國際單位制或其它單位制比較,自然單位制有優點,也有缺點:
簡化方程:借著設定基本物理常數為1,含有這些常數的方程會顯得更為簡潔,大多時候會更容易了解。例如,在狹義相對論里,能量與動量的關係式 E^2 = p^2*c^2 + m^2*c^4 似乎相當冗長,而 E = p + m 顯得簡單多了。
物理詮釋:自然單位制已經自己具備了量綱分析功能。例如,普朗克單位制的設計,已經囊括了量子力學和廣義相對論的一些性質。大約在普朗克長度的尺度,量子引力效應絕非湊巧地會開始變得重要。同樣地,在設計原子單位制時,已經考慮到電子的質量與電量。因此,描述氫原子的電子軌域的玻爾半徑理所當然地成為原子單位制的長度單位。
不需原器:“原器”(prototype)是一種用來定義單位的真實物體,例如國際千克原器(International Prototype Kilogram)是一塊存放於法國國際計量局的鉑銥合金圓柱體,其質量為1公斤。依賴原器有很多缺點:不可能實際複製出完全一樣的原器,真實物體會遭受腐蝕損壞,核對質量必需親自到法國跑一趟。自然單位制不需要參照到原器。
計量精密度較低:當初設計國際單位制時,一個主要目標是能夠適用於精密測量。例如,因為這躍遷頻率可以用原子鐘科技來精密複製,時間單位秒是使用銫原子的原子躍遷頻率來定義。自然單位制通常不是建立於可以在實驗室精密複製的物理量。所以,自然單位制的基本單位所具有的精密位數會低於國際單位制。例如,普朗克單位制所使用的重力常數G ,在實驗室里只能測量至4個有效數字。
意義過於籠統:構想採用普朗克單位制的方程 a = 10。假若 a 代表長度,則這方程的含意是 ;可是假若 a 代表質量,則這方程的含意是 a = 220kg。所以,假若變數 a 缺乏明確定義,則這方程很有可能被誤解。明顯不同地,採用國際單位制,對於方程 a = 10 ,假若 a 代表長度,則這方程的含意是 a = 10m ;假若 a 代表質量,則這方程的含意是 a = 10kg。從另一個角度來看,物理學者有時候會故意利用到這籠統性質。這時,自然單位制顯得特別有用。例如,在狹義相對論里,時間與空間的關係非常密切,假若,能夠不區分某變數所代表的是時間還是空間,或者,使用同一個矢量變數就可以一起代表時間與空間,這添加的功能會帶給理論學者很大的便利。
評價
粒子物理學中研究的主要是微觀高速現象,在研究中經常要考慮和處理量子效應和相對論效應,它們分別由啚和с體現。在粒子物理學中採用自然單位制可以把物理量和物理規律的物理意義比較直接地體現出來並使計算過程大大簡化。例如,在自然單位制中速度是無量綱的量,其數值的含義是等於以真空光速為單位所得到的值;又如,對於不穩定粒子,表現為有一個平均壽命τ,量子效應又決定其能級有一定寬度 寗,在自然單位制中,它們的關係簡單地為寗τ=1。在與粒子物理學密切有關的其他物理學科中,有時也採用自然單位制。

