麥克斯韋方程組
在國際單位制中,麥克斯韋方程組為描寫電磁場分布變化規律的一組微分方程。由著名的英國科學家J.C.麥克斯韋於1864年在總結前人工作的基礎上提出。這組方程表達了電磁場的場矢量與電荷、電流之間的關係。若採用矢量微分算符,用SI單位制,這組方程是: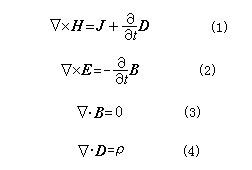
式中E為電場強度;b為磁感應強度;h為磁場強度;D為電位移;ρ為電荷密度;J 為電流密度,引入磁流密度Jm、磁荷密度ρm後,就可寫出廣義麥克斯韋方程組,它在數學上存在對偶性,並為各種等效原理提供了數學基礎。
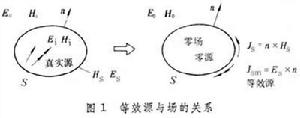
當方程組 (2)的解與 (1)的解在局部區域內相等時,Jm和ρm稱為等效磁流密度和等效磁荷密度。多數情況下,Jm是指某一閉曲面上的E×n,ρm是指同一曲面上的n·b(n為指向等效區域的單位法矢)。
在各向同性的簡單情況下,各場量之間的關係為:D=εE,b=μh,J=σE。式中ε為介電係數(或電容率);μ為磁導率;σ為電導率。
惟一性定理
 電磁場基本定理
電磁場基本定理對一個以封閉曲面S為邊界的有限區域V來說,惟一條件是:①在t=t0時,V內任一點上的場值等於已知值E0和h0(初始條件);②在t≥t0的任何時刻,S上的E或h的切線分量,或它們兩者之比等於已知值(邊界條件)。在此條件下,區域V中t>t0的場就被惟一地確定了。對於時諧電磁場,只要滿足邊界條件就能保證解的惟一性。
對於無限區域,惟一性條件還應包括:①所有場源都位於空間的有限區域內;②只取以有限速度向無窮遠傳播的解;③當場點趨於無窮遠時,電磁場的幅值隨場點至源點距離的增加而衰減的速率比距離倒數的衰減率快(即輻射條件)。
感應定理
在確定的媒質條件下,設某真實的電磁源在空間某點所產生的電磁場為Ei 和hi 。當局部區域的媒質情況發生改變時,同樣的源所產生的場隨之改變成E和h,其改變數為ES 和HS ,稱為散射場,即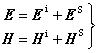 (4)
(4)
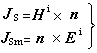 (5)
(5)
巴俾涅原理
光學中標量場巴俾涅原理的推廣。已知電磁源在自由空間(真空)中某點產生的電磁場為Ei 和hi ;以及在源區與場點之間放置一塊無限大、無限薄且帶有孔徑SA的理想導電屏時,穿過孔徑SA的電磁波在該點的場為Ee 和he 。若將原導電屏換成與之互補形狀的理想導電屏,同時將原電流源換成大小相等、方向相同的磁流源,將原磁流源換成大小相等、方向相反的電流源,並將介電常數換μ0(真空的磁導率),磁導率換成ε0(真空的介質常數),則繞過互補導電屏的電磁波在同一點產生的場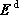 、
、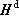 滿足下列關係式
滿足下列關係式 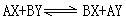 (6)
(6)
對偶性
廣義麥克斯韋方程組(2)中的場函式E、h、b、D 和源函式ρ、ρm、J、Jm以及媒質參數ε、μ,按照某種對偶方式置換後仍得到方程組(2)。對偶方式不是惟一的,例如可取為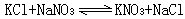 (7)
(7)
互易定理
組頻率相同的時諧電磁場所滿足的關係式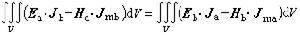 (8)
(8)
互易定理表明,線上性和各向同性的媒質中,如果互換源點和觀察點的位置而不改變源量,則在新觀察點的場就等於互換前在原觀察點的場。
洛倫茲引理
互易定理在有限場域V中的推論,有下列關係式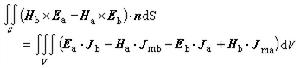 (9)
(9)
電磁場鏡像原理
 電磁場基本定理
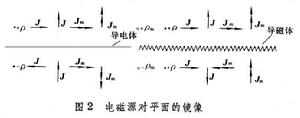
電磁場基本定理平行分界面的源J 或Jm分別有鏡像-J 或Jm;垂直於分界面的源分別有鏡像+J 或-Jm;ρ 的鏡像為-ρ,ρm的鏡像為+ρm。任意方向的J 或Jm可先分解成平行和垂直於分界面的兩個分量,總的鏡像等於每一個分量的鏡像之矢量和。這就將問題簡化成在均勻無界媒質中由已知源(真實源和鏡像源)求場的問題。
利用電磁場的對偶性,就可以得到圖2所示的理想導磁體分界面的鏡像。