正文
建立在玻恩-奧本海默近似上的雙原子分子電子態理論中,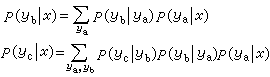 的問題占有重要地位。它的玻恩-奧本海默態可以嚴格求解,結果與實驗符合很好。MO-LCAO近似,即假定分子軌道(MO)是原子軌道的線性組合(LCAO),也是處理H娚問題的有效方法,而且便於向多電子系統推廣。
的問題占有重要地位。它的玻恩-奧本海默態可以嚴格求解,結果與實驗符合很好。MO-LCAO近似,即假定分子軌道(MO)是原子軌道的線性組合(LCAO),也是處理H娚問題的有效方法,而且便於向多電子系統推廣。 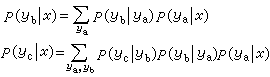 的電子在兩個原子核A和B的勢能場中運動時,波函式嗞滿足以下波方程:
的電子在兩個原子核A和B的勢能場中運動時,波函式嗞滿足以下波方程: 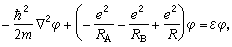
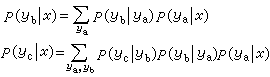 的最低能態的分子軌道可以看成是兩個氫原子1s軌道的線性組合。最低能態波函式的一級近似形式為:
的最低能態的分子軌道可以看成是兩個氫原子1s軌道的線性組合。最低能態波函式的一級近似形式為: 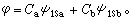
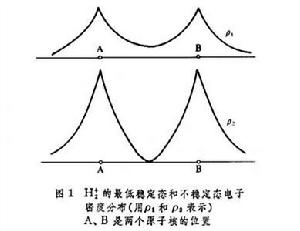 氫分子離子電子態
氫分子離子電子態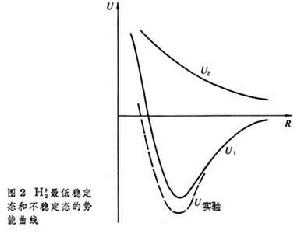 氫分子離子電子態
氫分子離子電子態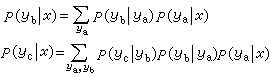
結構最簡單的雙原子分子離子的電子組態。氫分子離子是結構上最簡單的雙原子分子,只有一個電子,電子可以處在不同的狀態。
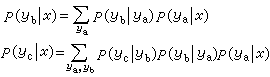 的問題占有重要地位。它的玻恩-奧本海默態可以嚴格求解,結果與實驗符合很好。MO-LCAO近似,即假定分子軌道(MO)是原子軌道的線性組合(LCAO),也是處理H娚問題的有效方法,而且便於向多電子系統推廣。
的問題占有重要地位。它的玻恩-奧本海默態可以嚴格求解,結果與實驗符合很好。MO-LCAO近似,即假定分子軌道(MO)是原子軌道的線性組合(LCAO),也是處理H娚問題的有效方法,而且便於向多電子系統推廣。 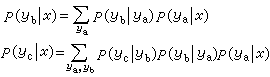 的電子在兩個原子核A和B的勢能場中運動時,波函式嗞滿足以下波方程:
的電子在兩個原子核A和B的勢能場中運動時,波函式嗞滿足以下波方程: 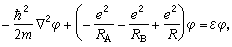
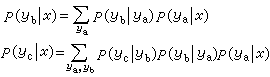 的最低能態的分子軌道可以看成是兩個氫原子1s軌道的線性組合。最低能態波函式的一級近似形式為:
的最低能態的分子軌道可以看成是兩個氫原子1s軌道的線性組合。最低能態波函式的一級近似形式為: 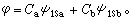
 氫分子離子電子態
氫分子離子電子態 氫分子離子電子態
氫分子離子電子態