LS 耦合
正文
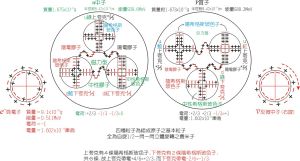 原子結構(含電子,質子,中子)-模型圖
原子結構(含電子,質子,中子)-模型圖 和自旋角動量
和自旋角動量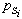 將分別受電子間靜電斥力和交換力(見交換作用)的作用各自耦合成總軌道角動量 pL和總自旋角動量ps,pL=
將分別受電子間靜電斥力和交換力(見交換作用)的作用各自耦合成總軌道角動量 pL和總自旋角動量ps,pL=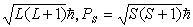 ,其中L、S分別為總軌道量子數和總自旋量子數,啚=h/2π,h為普朗克常數。
,其中L、S分別為總軌道量子數和總自旋量子數,啚=h/2π,h為普朗克常數。 以兩個非等效電子為例,其電子組態(n1l1,n2l2),n1、n2和l1、l2分別是兩電子的主量子數和軌道量子數,而電子自旋量子數都為1/2,即s1=s2=1/2。按原子的矢量模型,兩電子的軌道角動量的耦合
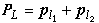 ,則L=
,則L=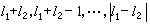 。自旋角動量的耦合
。自旋角動量的耦合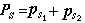 , 則 S=1,0。由各種可能的 S、L 值確定原子的多重譜項,不同譜項間能量差別相對來說比較大。而電子的自旋軌道磁相互作用又使pli和ps 耦合成原子總角動量pJ。
, 則 S=1,0。由各種可能的 S、L 值確定原子的多重譜項,不同譜項間能量差別相對來說比較大。而電子的自旋軌道磁相互作用又使pli和ps 耦合成原子總角動量pJ。 ,其中J 為總角動量量子數,
,其中J 為總角動量量子數,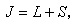
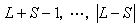 。由於假設這種磁相互作用遠小於電子間靜電作用,因此同一多重譜項由於自旋軌道磁相互作用而引起的不同J值的能態間距是很小的,通常稱為能級的精細結構。因此由LS 耦合形成的原子態的符號為2s+1 LJ。
。由於假設這種磁相互作用遠小於電子間靜電作用,因此同一多重譜項由於自旋軌道磁相互作用而引起的不同J值的能態間距是很小的,通常稱為能級的精細結構。因此由LS 耦合形成的原子態的符號為2s+1 LJ。 對於等效電子(見原子結構),耦合時要考慮泡利不相容原理,所形成的原子態要比非等效電子形成的少。例如兩個等效p電子經LS 耦合只能形成1 D2、3 P2,1,0、1 S0等五個原子態,而兩個非等效p電子卻可以形成3 D3,2,1、3 P2,1,0、3 S1、1 D2、1 P1、1 S0等十個原子態。
LS 耦合常適用於確定較輕元素原子的較低受激態和基態。對於重元素原子的受激態和輕元素原子的高受激態,則適用另一種稱為jj 耦合的近似方法。
LS 耦合有時也稱羅素-桑德斯耦合。
