概念
集合超積(ultraproduct of sets)是由一個集合族構成的集合。設I為一非空集合,D是I上一個真濾子,A(i∈I)為一族非空集合。令C={f:f為I上的函式且對每個i∈I,f(i)∈A}為諸A的卡氏積。記為:
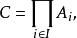 集合超積
集合超積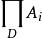 集合超積
集合超積對於C上的任意兩個函式f,g,如果{i∈I:f(i)=g(i)}∈D,則稱f和g是D等價的,記為f=g。容易看出,f是集合C上的一個等價關係。設f是f所在的等價類f={g∈C:f=g}。把關於f所有等價類的集合稱為諸A的以D為模的歸約積,記為。於是:
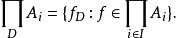 集合超積
集合超積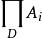 集合超積
集合超積特別地,如果D是I上的一個超濾子,則稱歸約積為超積。
集合
集合是現代數學的一個重要的基本概念。當我們把一組確定的事物作為整體來考察時,這一整體就叫做集合。
例如,(1)從1到10這10個自然數的全體;(2)小於100的所有質數的全體;(3)全體自然數;(4)一個班所有學生這一整體;(5)世界上所有國家組成的一個整體;等等,它們都是集合的例子。
上述例子可以看出,它們都是分別由不同的對象組成的一個整體,它們的特點是有確定的對象和具有一定的範圍。所以集合這個概念可以用以下的語言來描述:
集合是具有一定範圍的、確定的對象的全體。集合也簡稱為集。
在數學中,集合是一個不加定義的“原始概念”。這就是說,不能用比它更原始的概念去定義它。因此,集合在數學中被作為原始的最基本的概念來定義其它數學概念。集合是數學概念的出發點。
集合概念具有以下一些屬性:
(1)集合指的是一類事物的整體,而不是指其中的個別事物。
(2)集合中的任一對象具有確定性,即對於任何事物,可以通過某種法則確定其是否屬於某集合,或不屬於某集合,二者必居其一。(應指出,不具有這條屬性的,界限不清的集合是模糊集合。我們這裡所說的集合不是模糊集合,而是普通集合。)
(3)在一般情況下,約定一個集合中的各個對象是互不相同的。凡一個集合中所有相同的對象均應合併起來成為一個對象。例如,由1,1,2,2四個數組成的集合,應變成由1,2兩個數組成的集合。
(4)在一般情況下,集合只與組成它的成員有關,而與它的成員的順序無關。如由1,2,3,4組成的集合與由2,1,4,3組成的集合是同一個集合。
(5)一個集合不必由同一類事物作為它的對象。例如,由2, 3,a,b可以組成一個集合。
集合一般用大寫字母A,B,C,…表示。
集合族
在集合論和有關的數學分支中,給定集合 S的子集的蒐集 F叫做 S的子集族或 S上的集合族。更一般的說,無論什麼任何集合的蒐集都叫做集合族。
冪集P(S) 是在 S 上的集合族。 n 元素集合 S 的 k 元素子集 S(k) 形成了集合族。抽象單純復形是集合族。所有序數的類 Ord 是“大”集合族;它自身不是集合而是真類。
S 的任何子集族自身都是冪集P(S) 的子集。不論什麼集合族都是所有集合的真類(全集) V 的子類。超圖是集合 V (頂點集合)加上 V 的非空子集族(邊)。
濾子
濾子是集合論的基本概念之一。是由一個集合的某些子集組成的具有特定性質的集合。設I為一非空集合,S(I)是由I的所有子集構成的集合,如果D⊆S(I)適合下列諸條件:
1.I∈D;
2.若X,Y∈D,則X∩Y∈D;
3.若X∈D且X⊆Z⊆I,則Z∈D;
則稱D為定義在I上的一個濾子。濾子的例子是很多的,如平凡濾子D={I},非真濾子D=S(I)。對每個Y⊆I,稱濾子D={X⊆I:Y⊆X}為由Y生成的主濾子;濾子D={X∈S(I):I\X是I的有限子集}稱為自由濾子。如果D是I上的一個濾子,並且對任意的X∈S(I),X∈D,若且唯若I\X⋶D。則稱D是I上的一個超濾子。超濾子實質上是極大真濾子(即,D為I上的真濾子,並且在I上不存在真濾子F≠D.使得D⊆F)。濾子和理想有非常密切的關係。若I為集合S上的理想,則F={X⊂S:S\X∈I}為集合S上的一個濾子,稱之為I的對偶濾子,記為I。反之,若F為集合S上的濾子,則F={X⊂S:S\X∈F}為集合S上的一個理想,稱之為F的對偶理想。濾子概念也可以定義在偏序結構上。設〈P,≤〉為一偏序結構,F⊂P且滿足:
1.F非空;
2.若p≤q且p∈F,則q∈F;
3.若p,q∈F,則存在元素r∈F使r≤p且r≤q;
則稱F為偏序〈P,≤〉上的濾子。集合S上的濾子可以看成偏序〈P(S),⊆〉上的濾子。濾子有很多變體,但一般均可看成是某個特定偏序結構上的濾子。例如,布爾代數B上的濾子可以看成是偏序結構〈B\{0},≤〉上的濾子,這裡“≤”為布爾代數中定義的普通序關係。濾子概念在數理邏輯的其他領域以及抽象代數、拓撲學、微分幾何等現代數學分支中有著非常廣泛的套用。
極大濾子
亦稱超濾子。一類特殊的濾子。設F是集合X上的濾子。若對於包含F的濾子H恆有F=H,則稱F為極大濾子。對於集合X上的任意濾子F,恆存在包含F的極大濾子。若F為X上極大濾子,則對於任意AX,必有A∈F或X-A∈F。
集合論
基礎性的數學分支。.研究一般集合的大小、結構及集合之間的關係、運算,討論集合的計數、排序的方法以及建立各種無窮集的理論。雖然與集合理論有關的很多概念是早已有的,但是集合論的正式創立卻是起因於對無窮集討論的數學內部需要。
集合的思想可以追溯到古希臘的原子論學派。他們把直線看成一些原子的排列。在中世紀,就有人注意到這樣的事實:如果從兩個同心圓的中心出發作射線,那么這些射線就在兩個圓周上的點之間建立了一一對應,然而兩圓周的長度是不相等的。16世紀,伽利略(Galilei,G.)也發現正整數可以同正整數的平方構成一一對應。當時無窮集合的這一性質被看成與“整體大於部分”這一公理相悖,而稱為伽利略悖論。19世紀初,在傅立葉(Fourier,J.-B.-J.)、黎曼(Riemann,(G.F.)B.)、狄利克雷(Dirichlet,P.G.L.)的工作中,已經出現了由具有某些共同性質的點或函式構成的集合。但是他們都沒有進一步發展自己的思想。
19世紀初期,數學界對數學分析基礎的批判運動促進了集合論的誕生。1851年,波爾查諾(Bolzano,B.)發表著作《無窮悖論》,肯定了實無窮的存在,建立了集合等價的概念,還注意到了無窮集合的某些真部分有可能等價於整體的情況。但是為集合論奠定科學基礎並做出決定性貢獻的是康托爾(Cantor,G.F.P.)。促使他建立集合論的直接原因是函式的三角級數表示的惟一性問題。1870年,他應朋友海涅(Heine,H.E.)邀請開始研究這個問題。他在1871年至1872年的論文中逐步把三角級數展開的惟一性條件推廣到允許例外值成為無窮集的情況.他把函式間斷點問題的研究過渡到對點集本身的研究,明確地提出了點集、點集的導集、導集的導集等由實數構成的愈來愈複雜的集合。1873年12月7日,康托爾在給戴德金(Dedekind,J.W.R.)的信中說,他已成功地證明了實數集是不可數的.隨後,他的論文《論所有實代數數Z的一個性質》於1874年發表在克雷爾(Crelle,A.L.)的雜誌上。在這篇論文中包括了康托爾獨創的著名的對角線方法。康托爾在1874年提出集合的定義:“一個集合就是我們的直觀或我們的思想上那些確定的、能區分的對象(它們稱為集合的元素)匯集在一起,作為一個整體來考慮的結果。”這裡用匯集來定義集合實際上是同義語反覆.後來,人們認識到集合是一個原始的概念,不能用其他概念來定義,而只能加以描述或說明。但是這畢竟標誌著集合首次成了明確獨立的數學研究對象,集合論這個新的數學學科從此誕生。
