雅可比多項式

雅可比多項式是在區間【-1，1】上關於權函式組成正交系的多項式，又稱超幾何多項式。雅可比多項式在一些條件下可化為勒讓德多項式或切比雪夫多項式。

定義

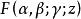雅可比多項式

雅可比多項式

雅可比多項式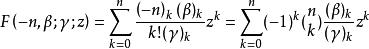

雅可比多項式

超幾何函式 在 或 等於負整數-n時是一個多項式 .

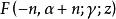雅可比多項式

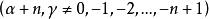雅可比多項式

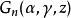雅可比多項式

稱為n次 雅可比多項式（也稱 超幾何多項式），記作 ；

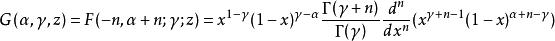雅可比多項式

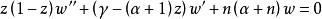雅可比多項式

它滿足雅可比微分方程 .

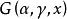雅可比多項式

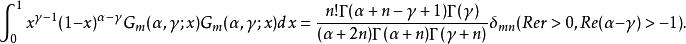雅可比多項式

的正交性

相關公式

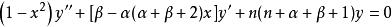雅可比多項式

微分方程：

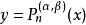雅可比多項式

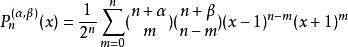雅可比多項式

顯式表達式： .

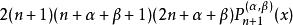雅可比多項式

遞推關係式：

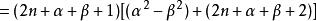雅可比多項式

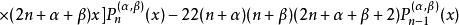雅可比多項式

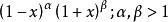雅可比多項式

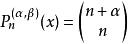雅可比多項式

權： 標準化：

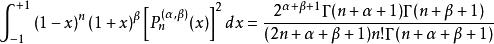雅可比多項式

模方：

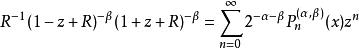雅可比多項式

母函式：

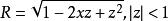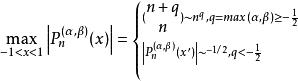雅可比多項式

雅可比多項式

雅可比多項式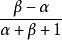

雅可比多項式

不等式：，是最接近的兩個極大值點之一。

特例

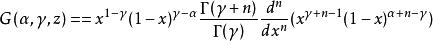雅可比多項式

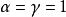雅可比多項式

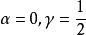雅可比多項式

公式中，當，它們可化為勒讓德多項式；時，它們可化為切比雪夫多項式。