定義
在數學中，特別是在數論中，除數函式是一個與整數除數相關的算術函式。 當被稱為除數函式時，它計算一個整數（包括1和數字本身）的除數。 它出現在許多顯著的身份中，包括關於黎曼ζ函式和愛森斯坦系列模組化形式。 除數函式由Ramanujan研究，他給出了一些重要的同餘和特徵，這些在Ramanujan的文章中分開處理。
一個相關的函式是除數求和函式，顧名思義，它是對除數函式的求和。
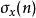除數函式除數函式定義為n的正因數的x次冪之和，即
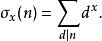除數函式例子
例如，σ(12) 是12的除數:
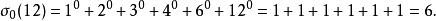除數函式當σ(12)是所有除數的和:
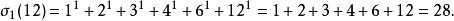除數函式而適當的除數的等分和s(12) :
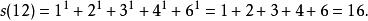除數函式特殊情況
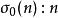除數函式的正因數的數目；
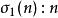除數函式的正因數之和（包括自己）。
| n/x | 0 | 1 | 2 |
| 1 | 1 | 1 | 1 |
| 2 | 2 | 3 | 5 |
| 3 | 2 | 4 | 10 |
| 4 | 3 | 7 | 21 |
| 5 | 2 | 6 | 26 |
| 10 | 4 | 18 | 130 |
| 12 | 6 | 28 | 210 |
| 20 | 6 | 42 | 546 |
| 25 | 3 | 31 | 651 |
性質
除數函式都是積性函式，但不是完全積性。
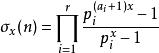除數函式
除數函式
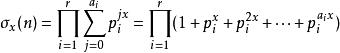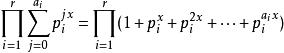除數函式，而這等式與相等，即n的各因數的x次方後的和，此式在x=1時即為n包括n本身在內的各因數的和。
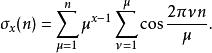除數函式
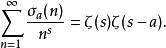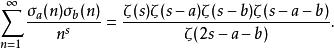除數函式
除數函式系列聯繫
涉及除數函式的兩個Dirichlet系列是：
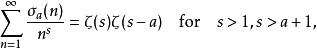除數函式當 d( n)= σ( n)是
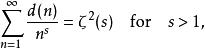除數函式和
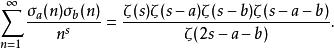除數函式涉及除數函式的Lambert系列是：
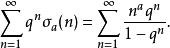除數函式其中 | q|≤1 和 a。這個總和也表現為愛森斯坦系列的傅立葉級數和Weierstrass橢圓函式的不變數。
