阿達馬,J.(-S.)

龐加萊的定性理論就是把常微分方程柯西問題的局部結果推廣到全局。 他的《變分學教程》一書奠定了泛函分析的基礎。 1964年在中國出版了他的著作《偏微分方程論》。
阿達馬,J.(-S.)
正文
 法國數學家。1865年12月8日生於凡爾賽,1963年10月17日卒於巴黎。1888年畢業於巴黎高等師範學校。先後在巴黎布豐中學、波爾多理學院和巴黎大學理學院任職。1909年到法蘭西學院任教,一直到退休(1937)。他長期在巴黎綜合工科學校和中央學校兼職任教,並在法蘭西學院創辦了一個著名的討論班。1912年被選為法國科學院院士。他還是蘇聯、美國、英國、義大利等國的科學院院士或皇家學會的會員以及許多國家的名譽博士。
法國數學家。1865年12月8日生於凡爾賽,1963年10月17日卒於巴黎。1888年畢業於巴黎高等師範學校。先後在巴黎布豐中學、波爾多理學院和巴黎大學理學院任職。1909年到法蘭西學院任教,一直到退休(1937)。他長期在巴黎綜合工科學校和中央學校兼職任教,並在法蘭西學院創辦了一個著名的討論班。1912年被選為法國科學院院士。他還是蘇聯、美國、英國、義大利等國的科學院院士或皇家學會的會員以及許多國家的名譽博士。
他早期就致力於把 A.-L.柯西在分析學上的局部理論推廣到全局。在復域裡其博士論文《泰勒級數所定義的函式的解析開拓》(1892)第一次把集合論引進複變函數論,更簡單地重證了柯西有關收斂半徑的結果;並探索了奇點在收斂圓上的位置及其性質,從而使收斂圓外的解析開拓更切實可行。這些成果至今仍是複變函數論的基本內容。他和他學生S.曼德爾勃羅伊合著《泰勒級數及其解析開拓》(1901)已成為經典著作。他在研究函式的極大模時得到了著名的三圓定理,並套用到整函式的泰勒級數係數極大模的衰減和這個函式的虧格間的關係上,完善了(J.-)H.龐加萊的結果,獲得了1892年法國科學院大獎。他還證明了黎曼ζ函式的虧格為零(1896),對黎曼猜想的解決作出了貢獻。證明了素數定理,即 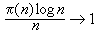 ,
,
從而建立解析數論的基礎。在實域裡,他的貢獻體現在常微分方程定性理論、泛函分析、線性二階偏微分方程定解問題和流體力學上。在常微分方程方面,他用不同的方法稍後於 Α.М.李亞普諾夫獨立地證明了有關穩定性的結果。龐加萊的定性理論就是把常微分方程柯西問題的局部結果推廣到全局。阿達馬認為這個推廣之所以成為可能,是因為龐加萊得到E.伽羅瓦用群處理代數方程解法的思想的啟示,這種思想使他關心並重視泛函分析工作。他線上性泛函的表示問題上的結果,開創里斯定理的先河。1908年他關於泛函微商問題的論文獲巴黎科學院獎,他在這篇論文中得到了Δu=0的格林函式的一個非線性積分方程的重要成果,他注意到這個方程與邊界s有關,而與方程無關,這至今還是泛函分析的一個重要課題。他的《變分學教程》一書奠定了泛函分析的基礎。1920年在泛函分析會議上作的報告《泛函分析所起的科學作用》是有影響的文獻。他的行列式定理在E.I.弗雷德霍姆的證明中居重要地位。在偏微分方程方面,他堅持柯西提倡的定解問題方向,明確了定解問題的含義,完善了適定性的要求。他得出根據二階方程的特徵表達式分型(橢圓、雙曲、拋物)的結論。那么,這三個型方程有沒有共同點呢?阿達馬提出了一般方程基本解的概念。有了基本解,模雙曲型方程的柯西問題的解,只要支柱是空向的,已給數據適當正規,就可以用一個發散積分的有限部分來表示。橢圓型方程就可以形成勢代表解,並通過這個勢滿足的弗雷德霍姆型積分方程求得狄利克雷問題的解。間接地求拋物型方程的基本解的步驟,也是由阿達馬提出來的。他不愧為線性二階偏微分方程理論的總結者、奠基者和開拓者。在流體力學方面的工作,大都包含在《波的傳播教程》一書里。在書中,他通過有關定解問題的討論,說明引進波的概念的必要性,對D.希爾伯特的重要工作,進行簡化和增補,對特徵理論做了詳盡的討論,從而指出方程組和單個方程有本質的不同,並在附錄中指出流體滑動的可能性。這些都在後來的氣動力學大範圍研究中起作用。
阿達馬曾在1936年來中國清華大學講學三個多月。1964年在中國出版了他的著作《偏微分方程論》。配圖
相關連線
 法國數學家。1865年12月8日生於凡爾賽,1963年10月17日卒於巴黎。1888年畢業於巴黎高等師範學校。先後在巴黎布豐中學、波爾多理學院和巴黎大學理學院任職。1909年到法蘭西學院任教,一直到退休(1937)。他長期在巴黎綜合工科學校和中央學校兼職任教,並在法蘭西學院創辦了一個著名的討論班。1912年被選為法國科學院院士。他還是蘇聯、美國、英國、義大利等國的科學院院士或皇家學會的會員以及許多國家的名譽博士。
法國數學家。1865年12月8日生於凡爾賽,1963年10月17日卒於巴黎。1888年畢業於巴黎高等師範學校。先後在巴黎布豐中學、波爾多理學院和巴黎大學理學院任職。1909年到法蘭西學院任教,一直到退休(1937)。他長期在巴黎綜合工科學校和中央學校兼職任教,並在法蘭西學院創辦了一個著名的討論班。1912年被選為法國科學院院士。他還是蘇聯、美國、英國、義大利等國的科學院院士或皇家學會的會員以及許多國家的名譽博士。 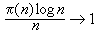 ,
,
