阿貝爾恆等式
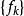 阿貝爾變換
阿貝爾變換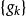 阿貝爾變換
阿貝爾變換阿貝爾變換(英語:Summation by parts)也叫 分部求和法(英語:Abel transformation,有別於Abel transform)或 阿貝爾引理(英語:Abel's lemma)是求和的一種方法。設 和 為兩個數列,則有
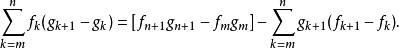 阿貝爾變換
阿貝爾變換它被用來證明積分第二中值定理。
分部求和公式也可被寫成比較對稱的方式:
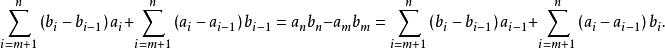 阿貝爾變換
阿貝爾變換積分第二中值定理
積分第二中值定理是與積分第一中值定理相互獨立的一個定理,屬於積分中值定理。它可以用來證明Dirichlet-Abel反常Riemann積分判別法。
內容
若g,(f·g)均在[a,b]上Riemann可積且f(x)在[a,b]上單調,則存在[a,b]上的點ξ使
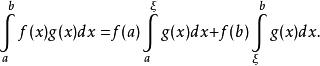 阿貝爾變換
阿貝爾變換退化態的幾何意義
令g(x)=1,則原公式可化為:存在[a,b]上的點ξ使
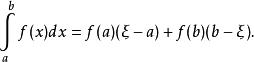 阿貝爾變換
阿貝爾變換分部積分法
概述
分部積分法是種積分的技巧。它是由微分的乘法定則和微積分基本定理推導而來的。其基本思路是將不易求得結果的積分形式,轉化為等價的但易於求出結果的積分形式。
規則
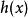 阿貝爾變換
阿貝爾變換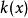 阿貝爾變換
阿貝爾變換假設 與 是兩個連續可導函式。由乘積法則可知
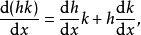 阿貝爾變換
阿貝爾變換對上述等式兩邊求不定積分,移項整理,得不定積分形式的分部積分方程
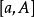 阿貝爾變換
阿貝爾變換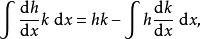 阿貝爾變換
阿貝爾變換由以上等式我們可以推導出分部積分法在區間的定積分形式
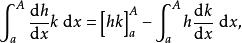 阿貝爾變換
阿貝爾變換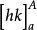 阿貝爾變換
阿貝爾變換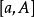 阿貝爾變換
阿貝爾變換已經積出的部分 可以代入上下限 表示為以下等式,
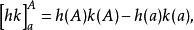 阿貝爾變換
阿貝爾變換而以上這條等式可以通過函式求導乘積法則,以及微積分基本定理通過以下方式倒推並得以驗證
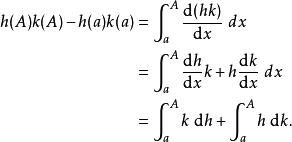 阿貝爾變換
阿貝爾變換在傳統的微積分教材里分部積分法通常寫成不定積分形式:
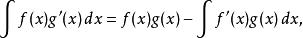 阿貝爾變換
阿貝爾變換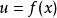 阿貝爾變換
阿貝爾變換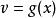 阿貝爾變換
阿貝爾變換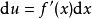 阿貝爾變換
阿貝爾變換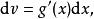 阿貝爾變換
阿貝爾變換如果更簡單些,令 、 ,微分 和 ,就可以得到更常見到的形式:
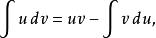 阿貝爾變換
阿貝爾變換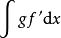 阿貝爾變換
阿貝爾變換注意,上面的原式中含有 g的導數;在使用這個規則時必須先找到不定積分 g,並且積分 必須是可積的。
在級數的離散分析中也可以用到類似的公式表達,稱為分部求和。
另一可用的表達方式可以將原表達方式里的因子僅寫成 f和 g,但缺點是引進了鑲套積分:
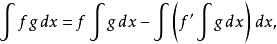 阿貝爾變換
阿貝爾變換這個表達方式只有當 f是連續可導而且 g是連續是才有效。
在黎曼-斯蒂爾吉斯積分和勒貝格-斯蒂爾吉斯積分有更多分部積分的公式。
提示:部分積分下面這樣更複雜一點的積分運算里也是有效的:
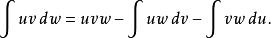 阿貝爾變換
阿貝爾變換套用
通過阿貝爾變換,可以分別證明任意項級數收斂的阿貝爾判別法和狄利克雷判別法。
