背景
隨著從存儲系統的日益複雜,對存儲系統的性能分析就顯得非常必要。單個存儲器的性能由生產廠商在數據手冊中說明,那么由多個存儲體構成的並行存儲系統的性能如何分析,尤其是系統的吞吐率及相應時間就必須藉助數學模型進行分析,或者再利用軟體進行仿真確定。對於更全面的系統仿真將花費非常大的代價,因此實際上多採用數學模型的方式確定。為此,利用阿姆達爾定律來說明存儲系統性能分析模型。
簡介
Amdahl加速定律的基本出發點是:1.對於很多科學計算,實時性要求很高,即在此類套用中時間是個關鍵因素,而計算負載是固定不變的。為此在一定的計算負載下,為達到實時性可利用增加處理器數來提高計算速度;2.因為固定的計算負載是可分布在多個處理器上的,這樣增加了處理器就加快了執行速度,從而達到了加速的目的。在此意義下,1967年Amdahl推導出了固定負載的加速公式。
阿姆達爾定律是計算機系統設計的重要定量原理之一,於1967年由IBM360系列機的主要設計者阿姆達爾首先提出。該定律是指:系統中對某一部件採用更快執行方式所能獲得的系統性能改進程度,取決於這種執行方式被使用的頻率,或所占總執行時間的比例。阿姆達爾定律實際上定義了採取增強(加速)某部分功能處理的措施後可獲得的性能改進或執行時間的加速比。簡單來說是通過更快的處理器來獲得加速是由慢的系統組件所限制。
阿姆達爾曾致力於並行處理系統的研究。對於固定負載情況下描述並行處理效果的加速比s,阿姆達爾經過深入研究給出了如下公式:
S=1/(1-a+a/n)
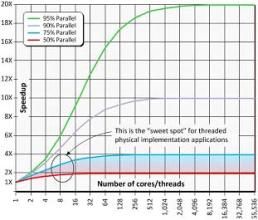
其中,a為並行計算部分所占比例,n為並行處理結點個數。這樣,當1-a=0時,(即沒有串列,只有並行)最大加速比s=n;當a=0時(即只有串列,沒有並行),最小加速比s=1;當n→∞時,極限加速比s→ 1/(1-a),這也就是加速比的上限。例如,若串列代碼占整個代碼的25%,則並行處理的總體性能不可能超過4。這一公式已被學術界所接受,並被稱做“阿姆達爾定律”,也稱為“安達爾定理”(Amdahl law)。
並行存儲性能中的阿姆達爾定律
並行存儲系統的性能分析可以通過簡單的性能模型展開,這其中主要就是阿姆達爾定律。阿姆達爾定律是一個非常簡單而通用的並行處理性能模型。這裡以程式的並行運行為例說明該定律,其他情況比較容易進行推推導分析。由於單個程式內部不一定全部可以實現並行處理。那么假設f為程式中必須進行串列操作的部分比率,其餘的1-f部分則認為可以完全在硬體上並行執行,而且P表示硬體的並行度。P在不同形式的計算機系統中代表著不同的含義:
(1)在MIMD系統中,P是處理器的數目;
(2)在SIMD系統中,P是正在處理的數據數目;
(3)在流水方式工作的SIMD系統中,P是矢量速度和標量速度的比;
(4)在流水方式工作的MIMD系統中,P是流水線功能段的數目。
為了在並行度p的硬體上獲得50%以上的效率,穿行操縱部分比率不能超過1/(P-1)。隨著P的增加,相應條件也越來越難以滿足。最早套用Amdahl定律對串列處理進行性能評價,但是在各種並行工作環境中Amdahl定律也非常有用。例如:在並行度很高的系統中,輕微的非並行代碼會對系統帶來很大的影響;快速的矢量處理器必須具有一個快速的標量處理器以獲得其峰值性能的相當大部分能力;對當前穿行執行的小部分代碼進行並行完成也可以增加相當大的效率。
雖然Amdahl定律建立了一個非常簡單的行囊模型,但也不能過於簡單化使用。系統規模,特別是處理器數目P通常為了處理更大的問題而不斷增加,而通常問題的規模的增加並不能顯著增加串列工作量。這種情況下,f與問題大小成反比。如果問題大小歲並行度P增加而增大,那么隨著問題和系統規模的增大,性能表現呈現出收縮性。在計算機系統中,Amdahl定律也可表述為,對系統內某部分的並行化改進造成的整體性能提升量取決於該部分在整體過程中執行的時間,即經常性事件或其部分的改進造成的整體性能得到較大提升。加速比也可以表示為使用改進方式完成整個任務時間的比值。實際上有兩個主要因素影響加速比,第一個因素是需要改進提高速度部分在總執行時間中所占的比值。實際上有兩個主要因素影響加速比,第一個因素是需要改進提高速度部分在總執行時間中所占的比例。譬如,1s完成的人物其中有200ms可以改進,那么該比例救贖20%,可以稱為改進比例。第二個因素是採用改進方式後相應部分速度提高的程度。可以用未改進情況下該部分執行時間與改進後執行時間的比值衡量。改進加速比一般都大於1。那么改進後的任務總時間為沒有改進的部分執行時間和改進部分執行時間的和。