定義
加速比以如下公式定義：
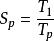加速比其中：
加速比指CPU數量
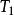加速比指順序執行算法的執行時間
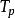加速比指當有p個處理器時，並行算法的執行時間
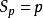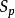加速比
加速比當 時， 便可稱為“線性加速比”（英語：linear speedup，又名“理想加速比”）。當某一併行算法的加速比為理想加速比時，若將處理器數量加倍，執行速度也會加倍，即如“理想”之意，有“優秀的可擴展性”。
“效率”
由加速比派生出的效率（英語：efficiency）則是量度性能的指標，並如下定義：
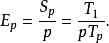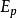加速比
加速比效率 的值一般介於0～1之間，用於表示在解決問題時，相較於在通信與同步上的花費，參與計算的處理器得到了什麼程度的充分利用。由定義易見，擁有線性加速比的算法與在單處理器上執行的算法的效率為1。
超線性加速比
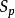加速比 加速比 加速比在並行計算過程中，有時會遇到加速比 比處理器數 更大的情況，此時求得的加速比即稱超線性加速比（英語：superlinear speedup）。超線性加速比很少出現，且由於初學者常以為理論上加速比的最大值應與參與計算的處理器的總數 相等，這一情況常使初學者迷惑不已。
並行計算加速比-阿姆達爾定律
阿姆達爾定律（英語：Amdahl's law，Amdahl's argument），一個計算機科學界的經驗法則，因吉恩·阿姆達爾而得名。它代表了處理器並行運算之後效率提升的能力。
特點：要求實時性，因此時間是關鍵因素，而計算負載是確定的。適用於固定計算負載。對於固定的問題規模，通過增加處理器，減少平均的計算負載，來提升運算速度。
並行計算中的 加速比是用並行前的執行速度和並行後的執行速度之比來表示的，它表示了在並行化之後的效率提升情況。
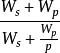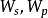加速比
加速比阿姆達爾定律是 固定負載（計算總量不變時）時的量化標準。可用公式： 來表示。式中 分別表示問題規模的串列分量（問題中不能並行化的那一部分）和並行分量，p表示處理器數量。
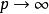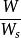加速比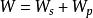
加速比
加速比只要注意到當 時，上式的極限是 ，其中， 。這意味著無論如何增大處理器數目，加速比是無法高於這個數的。
基於阿姆達爾定律和蘭特法則計算的加速比
評價多核CPU加速比已知模型的基礎上，基於第一性計算原理融合理解阿姆達爾定律和蘭特法則，提出描述多核CPU加速比的一個新模型．研究方法是從傳統的阿姆達爾定律切入，論述的邏輯順序分別基於約束固定任務，固定時間，存儲器和互連複雜性；兼顧了舉例論述同構多核的NoC頻寬性質和最大溫度特性．計算表明：基於固定時間模型與存儲器模型預測多核的加速能力，容易得到估計結果的樂觀上限；本文 提出的基於蘭特法則的模型計算結果，在並行比例較大時稍小於但接近前述模型估計值，而比固定任務模型的保守結果要好；NoC頻寬和最大溫度的結果提示，多(同構)核CPU期盼相對高的並行度架構。
並行處理中節點間通信對加速比的影響
加速比是衡量並行處理性能的重要指標之一; 較高加速比的獲得除與任務的劃分、並行算法的選擇等有關外 ,還與各節點間的通信有關; 在大多數並行系統中 ,在數據規模確定的情況下 ,程式的加速比隨節點數的增加而增加 ,但是大多數機群系統的節點間是共享物理傳輸介質的 ,這就使得許多並行程式的加速比在節點數目超過某一個值之後會隨著節點數的增加而減少;文章 通過數值實驗研究 ,分析了節點間通信對加速比的影響 ,進一步論證了節點間通信對加速比的重要影響。
