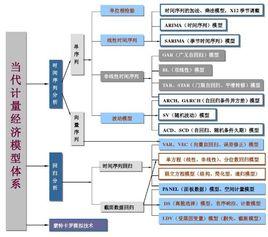
基本信息
門限自回歸模型是一類非線性模型，模型首先是由Tong和Lim提出的。門限自回歸模型在擬合實際數據時具有較好的性質，但是由於建立門限自回歸模型的步驟比較複雜，直到Tsay提出了相對比較簡易的建模及檢驗方法後，這類模型才被廣泛的套用。由於門限的控制作用，保證了模型具有很強的穩健性和廣泛的適用性，與多元線性回歸、模糊分析和灰色模型等預測模型相比，TAR模型具有預測精度高且穩健、套用簡便的特點，因此近年來TAR模型在經濟方面得到廣泛的套用 。
門限自回歸模型的模型形式與分段線性模型形式非常相似。門限或閾（Threshold）的概念是指高於或低於門限值（閾值）的自回歸過程不同，因此，可以捕捉到一個過程下降和上升模式中的非對稱性 。
思路及定義
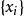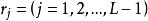門限自回歸模型
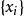門限自回歸模型 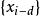門限自回歸模型
門限自回歸模型
門限自回歸模型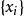 門限自回歸模型TAR的基本思路：在觀測時序 的取值範圍內引入L-1個門限值 ，將該範圍分成 L個區間，並根據延遲步數d將 按 值的大小分配到不同的門限區間內，再對不同區間內的 採用不同的自回歸模型來描述，這些自回歸模型的總和完成了對時序 整個非線性動態系統的描述。其一般形式為：
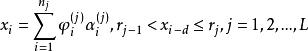門限自回歸模型
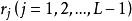門限自回歸模型
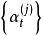門限自回歸模型
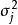門限自回歸模型
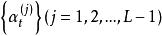門限自回歸模型
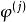門限自回歸模型
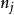門限自回歸模型 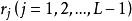門限自回歸模型
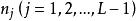門限自回歸模型
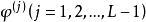門限自回歸模型其中， 為門限值，L為門限期間的個數；d為延遲步數； 對每一固定的j是方差為 的白噪聲系列，各 之間是相互獨立的； 為第j個門限區間自回歸係數； 為第j個門限區間模型的階數。由於TAR模型實質是分區間的AR模型，建模時沿用AR模型的參數估計方法和模型檢驗準則，如最小二乘法與AIC準則。其建模過程實質上是一個對d，L， ， 和 的多維尋優問題 。
特點
門限自回歸模型是具有廣泛意義的一種非線性時序模型，實質上是以分區間線性自回歸模型來描述研究對象在整個區間的非線性變化特性 。
門限自回歸模型作為一類非線性模型有其特有的性質。門限自回歸模型能夠解釋金融數據中經常表現出來的一些非線性性質周期性和不對稱性、波動的聚集性、波動的跳躍現象和時間的不可逆性。
不僅可以對序列本身做門限自回歸，建立最基本的模型，門限自回歸模型還可以和其它的模型混合使用，建立混合的模型。如人模型與的混合就是模型，這個混合模型彌補了模型在擬合實際數據中的不足 。
檢驗
門限自回歸非線性特徵檢驗
門限自回歸模型是在全局空間上對不同體制建立線性模型從而達到描述變數的非線性特徵的目的，但是一個變數到底應該建立線性模型還是應該建立非線性模型，需要有相應的檢驗標準才能讓人信服。早期，門限自回歸模型研究領域的研究重點之一就是門限效應的檢驗，並發展了許多可用的檢驗方法，這些檢驗方法的原假設一般是建立線性模型。它們可以大致分成兩類：一類是混合檢驗，另一類檢驗是針對某些特定的備擇假設模型所設計的。
（1）混合檢驗，即沒有指定的備擇假設模型，主要是檢驗對線性模型的偏離。關於混合檢驗，早期的有Ramsey (1969)提出的基於拉格朗日乘子原理的RESET檢驗、McLeod和Li (1983)關於模型殘差ARCH效應的檢驗以及Broock和Scheinkman等(1996)提出的檢驗殘差獨立性的BDS檢驗。
（2）針對某些特定的備擇假設模型所設計的檢驗。關於這類檢驗，備擇假設模型可以是平滑轉移自回歸模型((STAR)或門限自回歸模型(TAR)等。例如，Terasvirta (1994)研究了用Taylor展開式對LSTAR和ESTAR模型效應進行檢驗的方法。
事實上，在對門限自回歸的非線性特徵檢驗中，由於原假設和備擇假設中的參數不一致，會導致在原假設下推導得到的分布包含冗餘參數(在原假設下為不可識別參數)，進而導致分布函式不會隨著樣本容量增大漸近收斂到一個標準分布。Davies (1987)最早對該問題進行了研究，因此該問題也被稱為“Davies問題”。為了解決這個難題，有學者採用非參數的方法，也有學者提出採用綜合統計量的方法 。
