門限回歸模型的基本思想
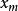 門限回歸模型
門限回歸模型預報對象y與預報因子集之間的一般門限回歸模型形式為:
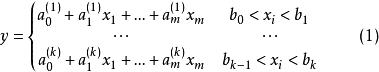 門限回歸模型
門限回歸模型 門限回歸模型
門限回歸模型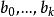 門限回歸模型
門限回歸模型式中,稱為門限變數,稱為門限閾值。在各段回歸方程中,入選的因子可以有所不同。
門限回歸模型的基本思想是通過門限變數的控制作用,當給出預報因子資料後,首先根據門限變數的門限闕值的判別控制作用,以決定不同情況下使用不同的預報方程,從而試圖解釋各種類似於跳躍和突變的現象。其實質上是把預報問題按狀態空間的取值進行分類,用分段的線性回歸模式來描述總體非線性預報問題。在直觀上此法可類比於用拆線分段逼近曲線,由於套用了分段線性化的思想,因此可以充分利用線性模式的處理手段 。
門限回歸模型的建模方法
 門限回歸模型
門限回歸模型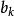 門限回歸模型
門限回歸模型如果我們已知門限變數和門限閾值,則根據門限變數值是否高於門限閾值來把樣本資料分為K段,分別對每一段樣本用線性逐步回歸來建模即可。在作預報時,根據門限變數實時資料,首先判斷其屬於哪一段,然後再用該段回歸模式代入預報因子實時資料即可作出預報。這些都是讀者熟知的常規線性統計預報計算分析方法了。由此可見,對門限回歸建模的關鍵是確定門限變數和門限閾值,這就是現在要重點討論的問題 。
根據門限回歸模型的思路,當門限變數值高於或低於門閾值時,將有顯著不同的預報關係。因而建模的步驟為:先找出門限變數和門限閾值,然後按此對樣本分組,分段建立線性模式。門限變數的確定有兩種情況,一種是基於對預報問題的物理分析,因果關係推斷,指定某個變數為門限變數,另一種情況是當對預報問題的物理原因不清、完全依靠統計方法時,可採下面的方法 。
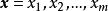 門限回歸模型
門限回歸模型 門限回歸模型
門限回歸模型 門限回歸模型
門限回歸模型 門限回歸模型
門限回歸模型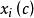 門限回歸模型
門限回歸模型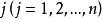 門限回歸模型
門限回歸模型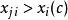 門限回歸模型
門限回歸模型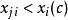 門限回歸模型
門限回歸模型我們先考慮只有一個門限閾值,即分為兩段回歸時的方法,然後再把它推廣到一般。設有預報對象y和m個預報因子,取n個樣本。從 x中任取一個因子,找出樣本中的最大值和最小值,求得的變化區間,在該區間內任給一個門限值記為,對每個樣本,把時所有的 x和y樣本分作一組子樣本,時所有的 x和y樣本分作另一組子樣本,然後對這兩組樣本分別建
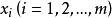 門限回歸模型
門限回歸模型 門限回歸模型
門限回歸模型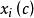 門限回歸模型
門限回歸模型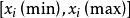 門限回歸模型
門限回歸模型立回歸方程, 於是就建立了一個門限回歸模型。窮盡所有可能的因子, 即取:,對窮盡所有可能的分段,即對門閾值,在內,取盡所有可能的值,於是就可建立所有可能的門限回歸模型,從中挑出效果最好的那一個,就是最優門限回歸模型 。
以上討論的門限回歸建模方法,在變數數和樣本數很少時,是易於實現的。但當變數數和樣本數較大時,其計算量就是目前一般微機難以完成的了。如果計算條件能充分滿足,顯然這種窮盡所有可能搜尋的計算方案是可以建立最佳廣]限回歸模型的。但在計算條件不能充分滿足的情況下,如何設計一些計算方案,在基於一定假設條件下,找到一個相對較好的門限回歸模型,就是一個需要認真討論的問題了。下面提供三種假設條件下的建模方案,供讀者在實際工作中參考選用。
1. 假設條件:門限變數和門限閾值是造成預報對象顯著差異的主要因子。此時要找到這樣的門限變數和門限閾值,當把預報對象分成兩組時,兩組預報對象間有最顯著的差異,由此建立的門限回歸模型,當預報關係發生改變時,預報對象有顯著差異。此種情況下的計算方法為:
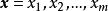 門限回歸模型
門限回歸模型 門限回歸模型
門限回歸模型設有y和,取n個樣本,從 x中任取一個因子,把它的樣本與y的樣本列為下表:
 門限回歸模型
門限回歸模型 門限回歸模型
門限回歸模型 門限回歸模型
門限回歸模型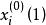 門限回歸模型
門限回歸模型找出的最大值和最小值,得出的變化區間,在該區間內給定一個門限初值,記為(上標0表示初值,下標i 表示第i個變數,括弧(1)表示只有一個門限)。然後把
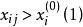 門限回歸模型
門限回歸模型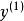 門限回歸模型
門限回歸模型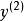 門限回歸模型
門限回歸模型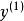 門限回歸模型
門限回歸模型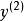 門限回歸模型
門限回歸模型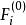 門限回歸模型
門限回歸模型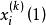 門限回歸模型
門限回歸模型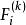 門限回歸模型
門限回歸模型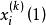 門限回歸模型
門限回歸模型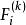 門限回歸模型
門限回歸模型 門限回歸模型
門限回歸模型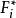 門限回歸模型
門限回歸模型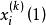 門限回歸模型
門限回歸模型上表中凡滿足 (j= 1,2...n)的那些預報對象樣本挑出來,組成一組子樣本,記為,其餘作為另一組子樣本, 記為。用方差分析方法,求得和這兩組子樣本的差異顯著性檢驗值,記為,然後運用一維搜尋來不斷調整門限初值,記為。按此法可不斷對y重新分組計算兩組樣本的差異顯著性檢驗值,記為,於是問題歸結為:對門限值尋優,使達到最大,從而求得以作為門限變數時的最大顯著性指標,記為相應的門限閾值記為。
 門限回歸模型
門限回歸模型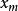 門限回歸模型
門限回歸模型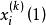 門限回歸模型
門限回歸模型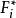 門限回歸模型
門限回歸模型對至每個因子都如此分析,於是求得每個因子的和,i=1,2,...,m,把它們排列如下:
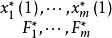 門限回歸模型
門限回歸模型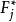 門限回歸模型
門限回歸模型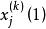 門限回歸模型
門限回歸模型從中挑出F的最大者,記為,其所對應的第j個因子,就是所求得的門限變數,相應的為門限閾值。 顯然,它滿足對門限變數原理假設:即在所有m個自變數中,可使模型預報關係及y有最大差異的那個變數。
對門限變數及門限閾值的求法,不限於這裡介紹的方差分析方法,還可運用其他方法,如最優分割法等。
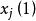 門限回歸模型
門限回歸模型找出門限變數x和門限閾值後,下一步就是把預報對象和預報因子樣本資料
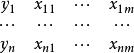 門限回歸模型
門限回歸模型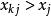 門限回歸模型
門限回歸模型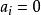 門限回歸模型
門限回歸模型按門限因子和門限閾值把滿足(k = 1,2..,n)的那些預報對象和預報因子樣本挑出來,組成一組子樣本, 其餘作為另一組子樣本, 然後分別對這兩組子樣本作線性逐步回歸,求得二段門限回歸模式為:(式中,未入選因子的係數)
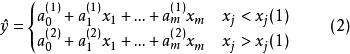 門限回歸模型
門限回歸模型這一建模方法不難推廣到分為L段的多元門限歸模型,現把建模方法簡述如下:
 門限回歸模型
門限回歸模型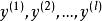 門限回歸模型
門限回歸模型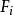 門限回歸模型
門限回歸模型(1)對因子,找出最大值和最小值,在其變化區間內取L個分點,把y劃分為L組,記為。運用方差分析方法,求得這L組的差異顯著性檢驗值,記為。
 門限回歸模型
門限回歸模型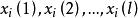 門限回歸模型
門限回歸模型(2)對區間中的L個分點,運用非線性參數尋優法,求得L個門限閾值, 記為使F達到最大。
 門限回歸模型
門限回歸模型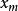 門限回歸模型
門限回歸模型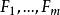 門限回歸模型
門限回歸模型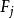 門限回歸模型
門限回歸模型 門限回歸模型
門限回歸模型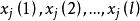 門限回歸模型
門限回歸模型(3)對至每一個因子重複(1)~(2)步,求得,從中找出最大值,記為,其所對應的因子即為門限變數,即為門限閾值。
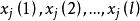 門限回歸模型
門限回歸模型 門限回歸模型
門限回歸模型(4)根據把y和的樣本分成L段,分別對每一段套用線性逐步回歸方法建立分段線性回歸方程,於是得到最終門限回歸模式如下:
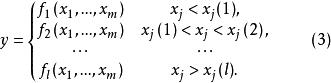 門限回歸模型
門限回歸模型2.假設條件:當預報關係發生改變時,門限變數值間有最顯著的差異。在此種情況下要找到這樣的門限變數和門限閾值, 使高於門限閥值和低於門限閾值的門限變數樣本值間有顯著差異,由此建立的門限回歸模型具有當預報關係發生改變時,門限變數值有顯著差異的特性。
 門限回歸模型
門限回歸模型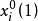 門限回歸模型
門限回歸模型 門限回歸模型
門限回歸模型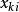 門限回歸模型
門限回歸模型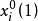 門限回歸模型
門限回歸模型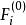 門限回歸模型
門限回歸模型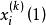 門限回歸模型
門限回歸模型此時具體計算方法為:從 X中任取一個因子,給定一個門限初值,把的樣本值 (k = 1,...,n)中大於的那些樣本分為一組,其餘的作為另一組,求得兩組數據的方差分析F值,記為然後套用一維搜尋來不斷調整門限初值,記為。
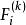 門限回歸模型
門限回歸模型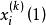 門限回歸模型
門限回歸模型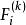 門限回歸模型
門限回歸模型 門限回歸模型
門限回歸模型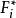 門限回歸模型
門限回歸模型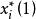 門限回歸模型
門限回歸模型以此不斷重新分組計算兩組樣本的差異顯著性檢驗值記為,對門限值尋優,使達到最大,從而求得以作為門限變數時的最大顯著性指標,記為,相應的門限閾值記為。以下各步驟同第-種假設條件下的計算方法,這裡從略。
3.假設條件:當預報問題為時間序列問題時,即樣本為時間序列樣本組成。此時假設預報對象時間序列由不同周期預報關係疊加組成。於是可把預報對象時間序列樣本進行周期分解。方法如下:
對 Y的n年樣本, 設周期為K,於是可排列成K年周期如下:
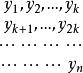 門限回歸模型
門限回歸模型把每一列作為一組子樣本,共有K組子樣本。對每-組子樣本的均值和方差與其他組進行比較,若存在顯著性差異,即可認為該組變數所對應的年份是由不同周期預報關係造成的,因而可把該組因變數所對應的樣本挑出來單獨建立一個回歸方程。其他樣本建立另一個回歸方程。在實際套用中,可對不同K值進行試驗,以確定顯著性最高的K年周期。
如果預報模型的突變受多個門限變數的控制,則稱為多重門限回歸,下面是兩個門限變數, 每個門限變數一個閾值的形式:
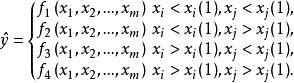 門限回歸模型
門限回歸模型其建模方法步驟不難仿照一個門限變數的分析方法進行推廣 。