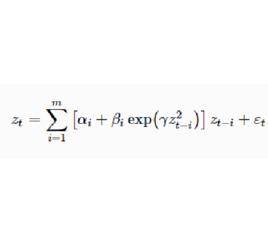EXAR模型結構及特點
EXAR模型源於二階非線性隨機振動微分方程
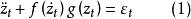 指數自回歸模型
指數自回歸模型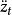 指數自回歸模型
指數自回歸模型 指數自回歸模型
指數自回歸模型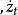 指數自回歸模型
指數自回歸模型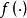 指數自回歸模型
指數自回歸模型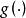 指數自回歸模型
指數自回歸模型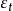 指數自回歸模型
指數自回歸模型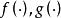 指數自回歸模型
指數自回歸模型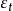 指數自回歸模型
指數自回歸模型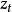 指數自回歸模型
指數自回歸模型式中, 表示對時間 的二階導數 元表示對時間t的一階導數;“阻尼力” 和“恢復力" 是非線性函式; 為獨立白噪聲。當 是線性函式時,則式(1)為二階線性微分方程。當 為白噪聲時,輸出 含有的周期隨振幅變化,即所謂的“頻幅相依”。尾崎根據上述效應提出了二階指數自回歸模型:
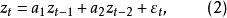 指數自回歸模型
指數自回歸模型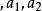 指數自回歸模型
指數自回歸模型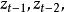 指數自回歸模型
指數自回歸模型式中 分別依賴於 這種依賴關係為指數函式形式:
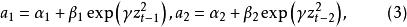 指數自回歸模型
指數自回歸模型推而廣之,m階EXAR模型的結構為:
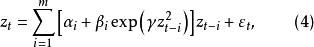 指數自回歸模型
指數自回歸模型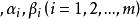 指數自回歸模型
指數自回歸模型 指數自回歸模型
指數自回歸模型式中 和 為模型參數。
EXAR模型的特點
EXAR模型的特點:
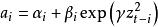 指數自回歸模型
指數自回歸模型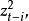 指數自回歸模型
指數自回歸模型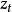 指數自回歸模型
指數自回歸模型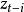 指數自回歸模型
指數自回歸模型①能刻畫非線性特性。模型參數 是隨時間變化的,其值取決於 同時又刻畫了 與 之間呈指數形式的非線性關係。
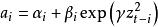 指數自回歸模型
指數自回歸模型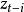 指數自回歸模型
指數自回歸模型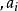 指數自回歸模型
指數自回歸模型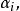 指數自回歸模型
指數自回歸模型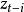 指數自回歸模型
指數自回歸模型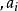 指數自回歸模型
指數自回歸模型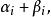 指數自回歸模型
指數自回歸模型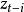 指數自回歸模型
指數自回歸模型②能產生突躍現象。從 中可看出,當 很大時 趨近於 而當 很小時 近似等於 其間變化關係是連續的。當 從最大值到最小值時就產生突躍現象。
EXAR模型參數估計
在非線性時間序列分析中,參數辨識的方法主要有最小二乘法、極大似然法等。哈根基於最小二乘法給出了EXAR模型的參數辨識方法:
 指數自回歸模型
指數自回歸模型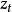 指數自回歸模型
指數自回歸模型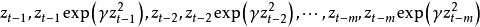 指數自回歸模型
指數自回歸模型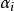 指數自回歸模型
指數自回歸模型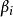 指數自回歸模型
指數自回歸模型(1) 先固定值,按最小二乘法作對的歸分析,估計和。用AIC確定模型階數m。
 指數自回歸模型
指數自回歸模型 指數自回歸模型
指數自回歸模型(2) 在一定範圍內取不同值,重複第(1)步的做法,得到不同值對應的參數和AIC值。
(3) 選擇AIC最小對應的模型參數即為所求。
上述參數辨識方法是可行的,但計算量大,且不一定能找到最優點,因而不是一種較好的方法。為此,提出了參數辨識的AGA,它包括如下兩個步驟:
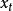 指數自回歸模型
指數自回歸模型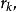 指數自回歸模型
指數自回歸模型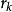 指數自回歸模型
指數自回歸模型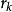 指數自回歸模型
指數自回歸模型第一步: 用自相關分析技術確定EXAR模型的自回歸項。時間序列延遲k步的自相關係數的方差隨k的增大而增大,的估計精度隨k的增加而降低,因此k應取較小的數值。
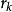 指數自回歸模型
指數自回歸模型 指數自回歸模型
指數自回歸模型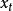 指數自回歸模型
指數自回歸模型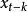 指數自回歸模型
指數自回歸模型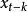 指數自回歸模型
指數自回歸模型根據的抽樣分布理論,在置信水平的情況下,推斷與之間的相依性是否顯著。EXAR模型的自回歸項應與這些相依性顯著的項相對應,其中相依性顯著的最大延遲步數即為模型的階數m。
第二步:用AGA直接在相對殘差平方和最小化下同時最佳化模型各參數,即求如下最小化問題:
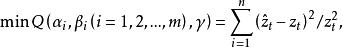 指數自回歸模型
指數自回歸模型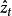 指數自回歸模型
指數自回歸模型式中,為擬合值 。