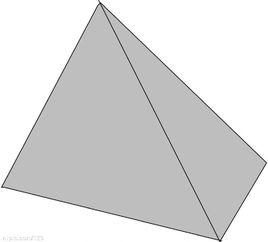
定義
圓錐(circular cone)和稜錐(pyramid)這樣的立體圖形是錐體。 以直角三角形的一個直角邊為軸鏇轉一周所得到的立體圖形就是圓錐。稜錐有三稜錐、四稜錐、五稜錐、六稜錐……
在非空集合C中，如果對任意的x屬於C和任意的a>0，有ax屬於C，則稱C是一個錐。若C同時也是凸集，則稱C是一個凸錐(convex cone)。此外，對於錐C，若0屬於C，則稱C為一個尖錐(pointed cone)。
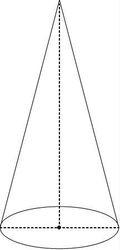圓錐
錐體錐體的體積=底面積×高×
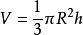錐體如圓錐即為： （R為底面圓的半徑，h為高）。
圓錐
概念
圓錐的高：圓錐的頂點到圓錐的底面圓心之間的距離叫做圓錐的高。
圓錐母線：圓錐的側面展開形成的扇形的半徑、底面圓周上任意一點到頂點的距離。
圓錐的側面積：將圓錐的側面沿母線展開，是一個扇形,這個扇形的弧長等於圓錐底面的周長，而扇形的半徑等於圓錐的母線的長。圓錐的側面積就是弧長為圓錐底面的周長×母線/2，沒展開時是一個曲面。
圓錐有一個底面、一個側面、一個頂點、一條高、無數條母線，且底面展開圖為一圓形側面展開圖是扇形。
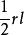錐體圓錐側面展開是一個扇形，已知扇形面積為，所以圓錐側面積為二分之一母線長×弧長（即底面周長）。另外，母線長等於底面圓直徑的圓錐，展開的扇形就是半圓。所有圓錐展開的扇形角度等於（底面直徑÷母線）×180度。
體積
一個圓錐所占空間的大小，叫做這個圓錐的體積。
錐體一個圓錐的體積等於與它等底等高的圓柱的體積的。
根據圓柱體積公式：
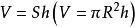錐體得出圓錐體積公式：
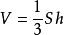錐體S是圓錐的底面積，h是圓錐的高，r是圓錐的底面半徑。
得出圓錐公式：
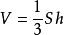錐體