基本概念
截錐體是一種與錐體有關的多面體,指由一平面去截一錐體而得的另一個錐體。錐體被不過頂點且與錐體母線都相交的平面所截,留下的在截面和底面間的錐體部分。常見的截錐體有圓台,稜台等,例如圓台體(圖2b):直角三角形ABC繞直角邊AC鏇轉一周,斜邊AB形成的空間軌跡所包圍的幾何體就是一個圓錐體,如圖2(a)所示。AB形成的表面叫圓錐面,AB為圓錐面的素線或母線。若圓錐體的頂端被截去一部分,就成為圓錐台或截錐體,如圖2(b)所示 。
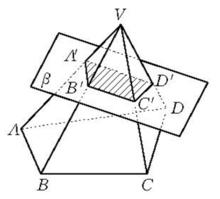 圖1(截錐體)
圖1(截錐體) 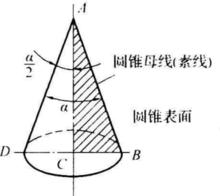 圖2(a) 圖2(a) | 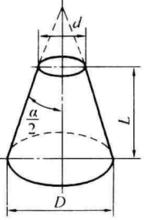 圖2(b) 圖2(b) |
截錐體舉例
圓台(平截圓錐體)
圓台亦稱正圓台或平截圓錐體,是一種特殊的台體,中國古算書稱圓亭、由平行於圓錐底面的平面截去圓錐上部小圓錐後留下的幾何體。截面和圓錐的底面稱為圓台的上、下底面,圓錐的軸、母線和側面的留下部分稱為圓台的軸、母線和側面,軸長稱為圓台的高。圓台也是直角梯形(如圖3中的梯形OOBB)繞一直角邊鏇轉一周而生成的幾何體,圖中⊙O,⊙O分別為圓台的上底、下底,AA,BB等為圓台的母線,線段OO的長為圓台的高 。
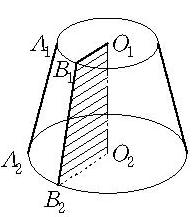 圖3
圖3圓台的主要性質是:
1.圓台的兩個底面都是圓,它們所在的平面平行。
2.平行於底面的截面都是圓。
3.圓台的母線都相等,它們延長相交於軸上同一點。
4.圓台的軸過兩個底面的圓心,並且垂直於兩底面,連結兩底面圓心的線段的長等於圓台的高。
5.圓台的軸截面是等腰梯形,它的兩腰是圓台的兩條母線,它的上、下底分別是圓台的上、下底面圓的直徑。
6.圓台的高、一條母線和經過這條母線兩個端點的上、下底面半徑組成一個直角梯形。
斜截圓錐體
斜截圓錐體是一種截圓錐體,用與所有母線均相交,且不與底面平行和相交的平面截去圓錐的錐尖部分,餘下的封閉幾何體稱為斜截圓錐,如圖4,圖5 為其三視圖。截交線為橢圓,再畫截交線的投影時,需先求出若干個共有點的投影,然後將它們依次光滑連線起來,才能獲得截交線的投影 。
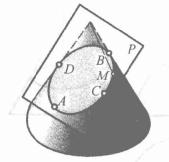 圖4
圖4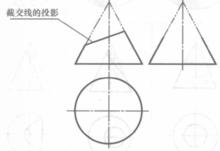 圖5
圖5稜台(平截稜錐)
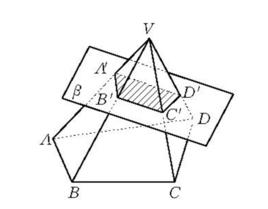
稜台亦稱角台或平截稜錐,是一種特殊的台體。即被截錐體是稜錐的台體。稜台底面的邊是稜台的底棱。稜錐被截時,側面餘下的梯形稱為稜台的側面,相鄰側面的交線稱為側棱,稜台側面梯形的高都稱為稜台的斜高,一般情況下各斜高不等.由三稜錐、四稜錐……n稜錐(n≥3,n∈N)截得的稜台分別稱為三稜台、四稜台……n稜台.稜台用它的兩底面的頂點字母表示,例如,五稜台記為稜台ABCDE-A′B′C′D′E′,或簡記為稜台AC′ 。
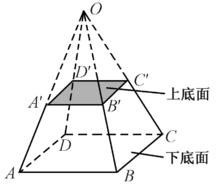 圖6
圖6稜台的主要性質有:
1.兩個底面是相似多邊形。
2.各側棱的延長線交於一點。
3.側面都是梯形。
4.對角面是梯形。
5.與稜台底面平行的截面是和底面相似的多邊形。
斜截稜錐
斜截稜錐與平截稜錐(即稜台)的區別是:平截稜錐的截面平行於底面,而斜截稜錐的截面是不與底面平行和相交的平面,如圖7為斜截稜錐的正視圖和俯視圖。
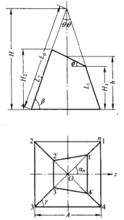 圖7
圖7截錐體的體積計算
截錐體的體積可用公式計算,也可用定積分計算 。
【例1】設有一截錐體,其上、下底均為橢圓,橢圓的軸長分別為2a,2b和2A,2B,高為h,求這截錐體的體積。
解 建立如圖8所示的坐標系,過y軸上y點作垂直於y軸的半面,則平面與截錐體
的截面為橢圓,易得其長短半軸分別為
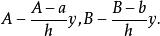 截錐體
截錐體截面的面積為
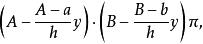 截錐體
截錐體於是截錐體的體積為
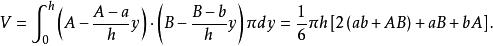 截錐體
截錐體