基本介紹
定義
量子糾纏量子糾纏是粒子在由兩個或兩個以上粒子組成系統中相互影響的現象，雖然粒子在空間上可能分開。
在物理學中，量子糾纏是指存在這樣一些態:一、A,B,C，…，在t<時，這些態之間不存在任何相互作用；二、當t>時，它們的狀態由Hibert空間（希爾伯特空間）HA，HB，HC...，中的矢量|Ψ(t)>A，|Ψ(t)>B，|Ψ(t)>C,…所描述，由A，B，C空間構成的量子系統ABC則由Hibert空間HABC...=.HA×HB×HC...中矢量|Ψ(t)>A，|Ψ(t)>B，|Ψ(t)>C所描述，則這樣的態被稱為比Hibert空間的直積態。否則稱態|Ψ(t)>A，|Ψ(t)>B，|Ψ(t)>C,.…是糾纏態。也就是說，如果存在糾纏態，就至少要有兩個以上的量子態進行疊加。
量子糾纏說明在兩個或兩個以上的穩定粒子間，會有強的量子關聯。例如在雙光子糾纏態中，向左（或向右）運動的光子既非左鏇，也非右鏇，既無所謂的x偏振，也無所謂的y偏振，實際上無論自鏇或其投影，在測量之前並不存在。在未測之時，二粒子態本來是不可分割的。
現象解釋
量子糾纏公式表達
1935年,愛因斯坦、波多爾斯基和羅森(EinsteinPodolskyandRosen)等人提出一種波,其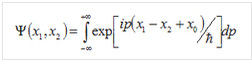量子態：
量子態其中x1，x2分別代表了兩個粒子的坐標，這樣一個量子態的基本特徵是在任何表象下，它都不可以寫成兩個子系統的量子態的直積的形式：
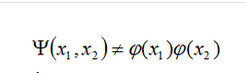量子態的直積的形式量子描述
量子糾纏於是，如何對糾纏定量化就顯得十分重要。但對於兩體純態而言，它仍是兩體純態唯一合理的糾纏度定義。對於多體糾纏度的描述的研究到目前為止仍沒有得到真正的解決，人們仍未放棄尋找一種物理意義上更為鮮明、簡單、易於求解的糾纏度的描述。
量子特點
量子力學是非定域的理論，這一點已被違背貝爾不等式的實驗結果所證實，因此，量子力學展現出許多反直觀的效應。量子力學中不能表示成直積形式的態稱為糾纏態。糾纏態之間的關聯不能被經典地解釋。所謂量子糾纏指的是兩個或多個量子系統之間存在非定域、非經典的強關聯。量子糾纏涉及實在性、定域性、隱變數以及測量理論等量子力學的基本問題，並在量子計算和量子通信的研究中起著重要的作用。
多體系的量子態的最普遍形式是糾纏態，而能表示成直積形式的非糾纏態只是一種很特殊的量子態。歷史上，糾纏態的概念最早出現在1935年薛丁格關於“貓態”的論文中。糾纏態對於了解量子力學的基本概念具有重要意義，近年來已在一些前沿領域中得到套用，特別是在量子信息方面。例如，量子遠程通信。
理論發展
理論產生
量子糾纏眾多的物理學家在自己觀點的指引下，對量子力學的基本解釋提出了自己的看法，主要有三種：傳統解釋、PTV系統解釋和統計解釋，這三種解釋之間既有區別又有聯繫。
傳統解釋出發點是量子假設，強調微觀領域內每個原子過程或基元中存在著本質的不連續，其核心思想是玻爾的互補原理（並協原理），還接受了玻恩對態函式的機率解釋，並把這種機率理解為是同一個粒子在給定時刻出現在某處的機率密度。PTV系統解釋的代表是玻姆，這種解釋試圖通過構造各種隱變數量子論來尋找量子力學的決定論基礎，即為態函式的機率解釋建構決定論的基石，目的是在微觀物理學領域內恢複決定論和嚴格因果性，消除經典世界同量子世界的獨特劃分，回到經典物理學的預設概念，建立物理世界的統一說明。統計解釋認為態函式是對統計系統的描述，量子理論是關於系統的統計理論，這個系統是由全同地(或相似的)製備的系統組成，不需要一個預先確定的動力學變數的集合，是一種最低限度的系統解釋。
上面講到三種觀點之間，是既有聯繫又有區別，正是由於各方都堅持己見，才有了著名的愛因斯坦與玻爾之間的論戰，量子糾纏才被愛因斯坦以一個悖論的疑問提出。量子糾纏就此提出。
1927年9月，玻爾在科摩會議中首度公開地演講他的互補原理，由於他採用了大量的哲學語言來闡釋互補原理，使大家感到震驚與困惑。當時大多數人對於測不準關係及互補原理的深刻內涵還不大明了。幾個星期後在布魯塞爾舉行的第五屆solvya會議，包括玻爾、愛因斯坦、玻恩、薛定愕、海森堡等世界最著名的科學家都出席了這項盛會。玻爾在會議中重述了他在科摩會議上的觀點。由於愛因斯坦並未參加科摩會議，這還是他首次聽到玻爾親自闡述互補原理和對量子力學的詮釋。
理論完善
1951年，玻姆在《量子理論》中重新表述了EPR思想，用兩個自鏇分量代替原來的坐標和動量，為進一步研究特別是實驗檢驗奠定了基礎。
1952年，玻姆在《物理學評論》上連續發表兩篇文章，提出了量子力學的隱變數解釋。玻姆認為，在量子世界中粒子仍然是沿著一條精確的連續軌跡運動的，只是這條軌跡不僅由通常的力來決定，而且還受到一種更微妙的量子勢的影響。量子勢由波函式產生，它通過提供關於整個環境的能動信息來引導粒子運動，正是它的存在導致了微觀粒子不同於巨觀物體的奇異的運動表現。玻姆理論最引人注目之處在於它對測量的處理。在這一理論中，量子系統的性質不只屬於系統本身，它的演化既取決於系統同時也取決於測量儀器。因此，關於隱變數的測量結果的統計分布將隨實驗裝置的不同而不同。正是這個整體性特徵保證了玻姆的隱變數理論與量子力學(對於測量結果)具有完全相同的預測。然而，它也導致了一個令人極不舒服的結果。根據玻姆理論的預言，儘管它為粒子找回了軌跡，但卻是一條永遠不可見的軌跡，理論中引入的隱變數—粒子的確定的位置和速度都是原則上不可測知的。人們永遠無法知道粒子實際的運動軌跡，對它們的測量將總是產生與量子力學相一致的結果。
此外，玻爾理論所假設的另一物理實在波函式同樣是不可探測的隱變數，因為對單個粒子的物理測量一般只產生一個關於粒子性質的確定的結果，而根本測不到任何平場的性質。
主要成果
糾纏態製備
量子糾纏2000年，美國國家標準局在離子阱系統上實現了四離子的糾纏態。
2004年，合肥微尺度物質科學國家實驗室量子物理與量子信息研究部的研究人員打破了這一紀錄，在國際上首次成功實現五光子糾纏的操縱。
2005年底，美國國家標準局和奧地利因斯布魯克小組分別宣布實現了六個和八個離子的糾纏態，並且一直保持著這個紀錄。
中科院量子信息重點實驗室李傳鋒、黃運鋒研究組在郭光燦院士的領導下，成功製備出八光子糾纏態——GHZ態，並進一步利用產生出的糾纏態完成了八連線埠量子通信複雜性實驗。實驗結果超越了以往界限，展示了量子通信抗干擾能力強、傳播速度快的優越性。研究工作於2011年11月22日線上發表在《自然·通訊》上。
量子態隱形傳輸
1997年，奧地利蔡林格小組在室內首次完成了量子態隱形傳輸的原理性實驗驗證。2004年，該小組利用多瑙河底的光纖信道，成功地將量子“逾時空穿越”距離提高到600米。但由於光纖信道中的損耗和環境的干擾，量子態隱形傳輸的距離難以大幅度提高。
2004年，中國科大潘建偉、彭承志等研究人員的小組早在2005年就在合肥創造了13公里的自由空間雙向量子糾纏“拆分”、傳送的世界紀錄，同時驗證了在外層空間與地球之間分發糾纏光子的可行性。2007年開始，中國科大——清華大學聯合研究小組在北京架設了長達16公里的自由空間量子信道，並取得了一系列關鍵技術突破，最終在2009年成功實現了世界上最遠距離的量子態隱形傳輸，證實了量子態隱形傳輸穿越大氣層的可行性，為未來基於衛星中繼的全球化量子通信網奠定了可靠基礎。該成果已經發表在2010年6月1日出版的英國《自然》雜誌子刊《自然·光子學》上，並引起了國際學術界的廣泛關注。
理論套用
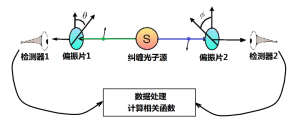量子糾纏