基本介紹
重極限是多元函式的一種極限,因為對n(≥2)元函式而言,極限
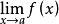 重極限
重極限中x=(x₁,x₂,…,x),a=(a₁,a₂,…,a)∈Rⁿ,x→a意味著同時有x₁→a₁,x₂→a₂,…,x→a,故稱相應的極限為 n重極限,作為多元函式特例的多重數列的極限也稱為 重極限 。如二重極限
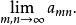 重極限
重極限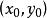 重極限
重極限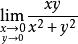 重極限
重極限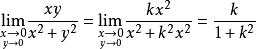 重極限
重極限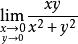 重極限
重極限證明重極限不存在常用的方法是證明沿兩種不同路徑極限不同(通常可取過點的直線)。例如證明重極限不存在,取直線y=kx,讓點(x,y)沿直線y=kx趨於(0,0)點此時有,則重極限不存在 。
求重極限
求重極限的常用方法有:
1)利用極限性質(四則運算法則,夾逼原理);
2)消去分母中極限為零的因子(有理化,等價無窮小代換);
3)利用無窮小量與有界變數之積為無窮小量 。
【例1】求下列極限
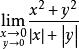 重極限
重極限(1);
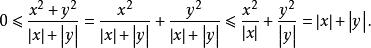 重極限
重極限解:(1)由於
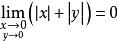 重極限
重極限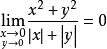 重極限
重極限而,由夾逼原理知.
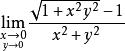 重極限
重極限(2).
解:(2)將分子有理化:
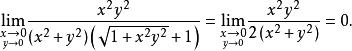 重極限
重極限原式=
重極限與累次極限的關係
多元實變函式f(p)=f(x,x,...,x),當它的所有變數同時取極限時函式值的極限,這種極限稱為 重極限。當自變數x,x,...,x不是同時取極限,而是依一定的順序相繼取極限時,f(x,x,...,x)的極限,稱為 累次極限。
例如,當p(x,y)為平面中的點時,設聚點A的坐標為(a,b),則f(P)在P→4時的重極限為
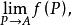 重極限
重極限我們也把它記作
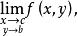 重極限
重極限而它的兩個累次極限則記為
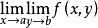 重極限
重極限與
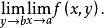 重極限
重極限重極限與累次極限的關係
(1)累次極限存在且相等時,重極限未必存在。
(2)重極限存在時,累次極限不一定存在。
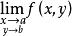 重極限
重極限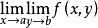 重極限
重極限(3)若與都存在,則二者必相等。
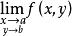 重極限
重極限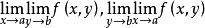 重極限
重極限(4)若與都存在,則三者必相等。
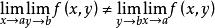 重極限
重極限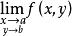 重極限
重極限(5)若,則不存在。
注意
1.對於二個不同變數的極限過程在交換其次序的時候,應該加以注意,不是無條件地都可以交換次序的。
2.累次極限和重極限的關係也是相當複雜的,不能把重極限存在(或累次極限存在且相等)認為是累次極限相等(或重極限序在)的必要條件 。

