定義和例子
定義1
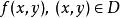 累次極限
累次極限 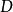 累次極限
累次極限  累次極限
累次極限 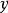 累次極限
累次極限 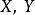 累次極限
累次極限 設 , 在 軸、 軸上的投影分別為 ,即
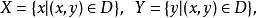 累次極限
累次極限 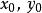 累次極限
累次極限 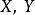 累次極限
累次極限 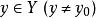 累次極限
累次極限 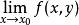 累次極限
累次極限 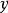 累次極限
累次極限 分別是 的聚點。若對每一個 ,存在極限 ,它一般與 有關,故記作
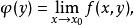 累次極限
累次極限 如果進一步還存在極限
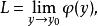 累次極限
累次極限 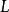 累次極限
累次極限  累次極限
累次極限 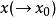 累次極限
累次極限 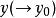 累次極限
累次極限 則稱此極限 為 先對 ,後對 的 累次極限 ,記作
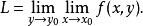 累次極限
累次極限 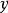 累次極限
累次極限  累次極限
累次極限 類似地可以定義先對 後對 的累次極限
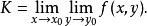 累次極限
累次極限 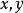 累次極限
累次極限 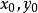 累次極限
累次極限 對於兩個自變數 同時以任何方式趨於 ,即
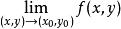 累次極限
累次極限 這種極限也稱為 重極限。
累次極限與重極限是兩個不同的概念,它們的存在性沒有必然的蘊含關係。下面兩個例子將說明這一點。
例1
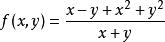 累次極限
累次極限 設 ,它關於原點的兩個累次極限分別為
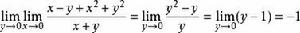 累次極限
累次極限 與
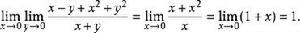 累次極限
累次極限 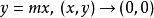 累次極限
累次極限 當沿斜率不同的直線 ,容易驗證所得極限也不同。因此該函式的重極限不存在。
例2
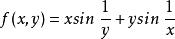 累次極限
累次極限 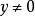 累次極限
累次極限 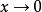 累次極限
累次極限  累次極限
累次極限 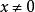 累次極限
累次極限 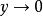 累次極限
累次極限  累次極限
累次極限 設 ,它關於原點的兩個累次極限都不存在。這是因為對任何 ,當 時 的第二項不存在極限。同理,對任何 ,當 時 的第一項也不存在極限。但是由於
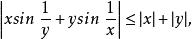 累次極限
累次極限  累次極限
累次極限 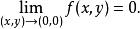 累次極限
累次極限 故 的重極限存在,且
重極限與累次極限之間的聯繫
定理1
 累次極限
累次極限 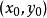 累次極限
累次極限 若 在點 存在重極限
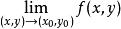 累次極限
累次極限 與累次極限
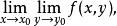 累次極限
累次極限 則它們必相等。
推論1
若累次極限
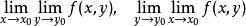 累次極限
累次極限 和重極限
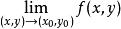 累次極限
累次極限 都存在,則三者相等。
推論2
若累次極限
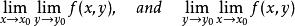 累次極限
累次極限 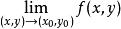 累次極限
累次極限 存在但不相等,則重極限
必不存在。定理1保證了在重極限與一個累次極限都存在時,它們必相等,但它們對另一個累次極限的存在性卻得不出什麼結論。
