定義性質
地球形狀的一級近似為圓球體，而二級近似為扁球體。對於理論目的來說，要選擇各處都是水平的一個面，即各處都垂直於擺線的一個面。這個面稱為水平面，或等位(equip-otential)面。測定地球形狀的問題就是測定所有等位面的問題。兩個等位面不能相交，而且在其中一個面上給出一個定點就將它完全固定。在海平面附近取一個標準點，就得到一個稱作大地水準面(geoid)的等位面。它是一個參考水平面，而且與任何其它等位面沒有什麼不同之處(除開在量綱上)。應該指出，一個等位面不能組成一個等重力面，例如，大洋面近似於一個等位面(各處都垂直於重力)，但大洋上的重力引力十分不同。
推導公式
重力理論1743年，法國數學家A．C．Clairaut得出在具有面形式的地球表面的不同點上測量重力有關的表達式。假定地球是-一個扁球體，其極坐標方程式給出為r=a（1-f ），此處f為該方程式定義的扁度。
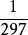重力理論 重力理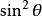論
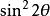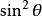重力理論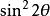 重力理論 重力理論取f= ，則下列公式可以計算出在任何地方的海平面重力值：g=978．049(1+0.0052884 -0.0000059 )，這就是國際重力公式(International gravity formula)。 項的常數包括幾何扁率與離心力效應。 項是對旋轉體假定的扁球形狀不相一致的校正。
使用人造地球衛星，已經可能提出地球重力場與地球形狀的輔助信息。如果地球嚴格地是圓球體，並且沒有大氣圈，則儘管由於太陽和太陽系中其它星體的微小攝動，衛星路徑還將是一個焦點在地球中心的橢圓。幸虧大氣圈和地球扁率造成的一級攝動十分明顯。
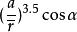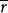重力理論
重力理論D．G．King-Hele(1958)曾證明，由於地球重力場不是球對稱的，以致引起三種主要的攝動。首先，軌道平面在方向上不再固定，但在衛星運動相反的方向中繞地球軸轉動，而仍保持與赤道成定角口的傾斜。轉動速率約為10.00 度/天，此處a為地球赤道半徑，而 為衛星離地球中心的諧和平均距離。
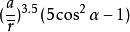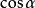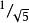重力理論
重力理論
重力理論
重力理論
重力理論地球扁率的第二個主要效應是軌道主軸在軌道平面內的緩慢轉動，以致軌道為具有轉動主軸的近似橢圓。轉動率約為5.00 度/天。在 = ，或 ≈度時，轉動速率消失。
科學探討
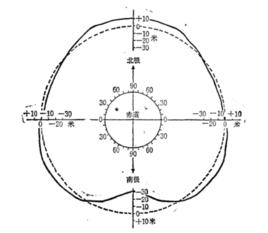
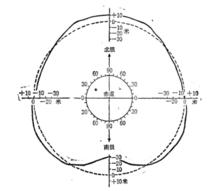大地水準面平均子午剖面相對於扁率1/198.25的圓球體的高度此衛星軌道偏心率中的周期變化也能夠用地球重力場中有第三種帶諧函式的存在來作解釋。這就改變了大地水準面，使它呈梨形（如圖）。此圖形使形狀受到很大的誇張，其變化僅是：在南極為30米，在北極為10米，而在中緯度地區內為7．5米。然而，存在這種大小的第三個諧和函式指出在地球表面上有一個很大的負荷。所包含的應力必須得到大於通常對地球內部所假定的機械強度，或者受到在地幔中大尺度的對流流的支持。大地水準面的低洼地區為近來被冰覆蓋並迅速上升之處，而J．T．Wilson(1960)曾指出，沒有證據說明地球將長期保持梨狀。A．H．Cooke(1963)已經給出利用衛星測定地球重力位的詳細討論。為了求得比單獨根據衛星資料所得更為完整的地球重力場圖形，W．H．Kaule(1966)和R．H．Rapp(1968)已經將衛星資料與重力資料聯合起來。Rapp對於沒有重力觀測存在的地區使用模擬異常，而Kaule對這種地區使用統計預測。
