定義
遞歸定義是數理邏輯和計算機科學用到的一種定義方式,使用被定義對象的自身來為其下定義(簡單說就是自我複製的定義)。遞歸定義與歸納定義類似,但也有不同之處。遞歸定義中使用被定義對象自身來定義,而歸納定義是使用被定義對象的已經定義的部分來定義尚未定義的部分。不過,使用遞歸定義的函式或集合,它們的性質可以用數學歸納法,通過遞歸定義的內容來證明。
定義方式
大部分的遞歸定義都由三個部分構成:基本情況的定義,遞歸法則和遞歸結束的情況。如果定義的對象是無限的,那么可以省略第三個部分(遞歸結束的情況)。比如說,可以用遞歸定義的方式來定義如下的一個自然數集上的函式f:
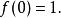 遞歸定義
遞歸定義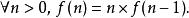 遞歸定義
遞歸定義這個定義在邏輯上是成立的,因為它首先定義了f在最小的自然數0上的取值,接下來對每個大於零的自然數n,只要重複有限多次定義的過程,最終就會回到對0的定義上。這樣定義出的函式f就是階乘函式。
遞歸定義和循環定義的不同之處在於,後者不包括對基本情況的定義。比如定義建立在整數集上的函式g:
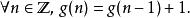 遞歸定義
遞歸定義則我們永遠無法確定g的取值,這便是循環定義。
構成
它由兩個部分組成:
1.初始條件:列出哪些個體屬於一個給定的集合,
2.歸納條件:當在條件中列出的個體屬於給定集合時,則另一些個體也屬於該集合。
舉例
例如,在命題邏輯中,合式公式定義為:
合式公式是按以下規則構成的有窮長符號串:
1.每個原子公式是合式公式,
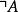 遞歸定義
遞歸定義2.若A是合式公式,則是合式公式,
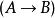 遞歸定義
遞歸定義3.若A,B是合式公式,則是合式公式,
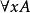 遞歸定義
遞歸定義4.若A是合式公式,x是變元,則是合式公式。