基本介紹
遞推是按照一定的規律來計算序列中的每個項,通常是通過計算前面的一些項來得出序列中的指定項的值。其思想是把一個複雜的龐大的計算過程轉化為簡單過程的多次重複,該算法利用了計算機速度快和不知疲倦的機器特點。
遞推算法
【例1】
植樹節那天,有五位同學參加了植樹活動,他們完成植樹的棵樹都不相同。問第一位同學植了多少棵時,他指著旁邊的第二位同學說比他多植了兩棵;追問第二位同學,他又說比第三位同學多植了兩棵;... 如此,都說比另一位同學多植兩棵。最後問到第五位同學時,他說自己植了10棵。到底第一位同學植了多少棵樹?
分析:設第一位同學植樹的棵樹為a1,欲求a1,需從第五位同學植樹的棵數a5入手,根據“多兩棵”這個規律,按照一定順序逐步進行推算:
(1) a5=10;
(2) a4=a5+2=12;
(3) a3=a4+2=14;
(4) a2=a3+2=16;
(5) a1=a2+2=18;
Pascal程式:
Program Examl;
Var i,a:byte;
begin
a:=10;
for i:= 1 to 4 do
a:=a+2;
writeln('The Num is' ,a);
readln;
end.
本程式的遞推運算可用下圖示表示:
初始值a:=10 ----- i=1,a=a+2(12) ----- i=2,a=a+2(14) ------ i=3,a=a+2(16) ----- i=4,a=a+2(18) ---- 輸出a值
例2:
十本不同的書放在書架上。現重新擺放,使每本書都不在原來放的位置。有幾種擺法?
當n個編號元素放在n個編號位置,元素編號與位置編號各不對應的方法數用M(n)表示,那么M(n-1)就表示n-1個編號元素放在n-1個編號位置,各不對應的方法數,其它類推.
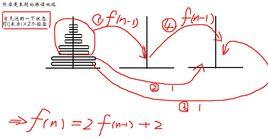
第一步,把第n個元素放在一個位置,比如位置k,一共有n-1種方法;
第二步,放編號為k的元素,這時有兩種情況.1,把它放到位置n,那么,對於剩下的n-2個元素,就有M(n-2)種方法;2,不把它放到位置n,這時,對於這n-1個元素,有M(n-1)種方法;
綜上得到
M(n)=(n-1)[M(n-2)+M(n-1)]
遞推算法以初始(起點)值為基礎,用相同的運算規律,逐次重複運算,直至運算結束。這種從“起點”重複相同的方法直至到達一定“邊界”,猶如單向運動,用循環可以實現。遞推的本質是按規律逐次推出(計算)先一步的結果。