定義
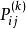 遍歷性
遍歷性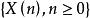 遍歷性
遍歷性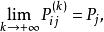 遍歷性
遍歷性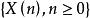 遍歷性
遍歷性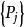 遍歷性
遍歷性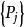 遍歷性
遍歷性設 為齊次馬氏鏈 的k步轉移機率,如果對一切i,j,存在不依賴於i的極限 則稱馬氏鏈 具有遍歷性,若 構成一個機率分布,則稱該馬氏鏈存在著極限分布 。
遍歷定理
定理1
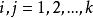 遍歷性
遍歷性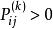 遍歷性
遍歷性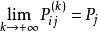 遍歷性
遍歷性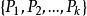 遍歷性
遍歷性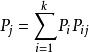 遍歷性
遍歷性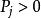 遍歷性
遍歷性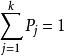 遍歷性
遍歷性對於有限狀態齊次馬氏鏈,如果存在正整數s,並且對所有的 都有 成立,則該馬氏鏈必具有遍歷性,且式 中的 即為極限分布,它的方程組 滿足條件 , 的唯一解。
定理2
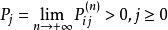 遍歷性
遍歷性不可約非周期的可列狀態其次馬氏鏈存在平穩分布的充要條件是,這個鏈的所有狀態都是正常返的,且這時極限分布 是唯一的平穩分布。
例題分析
1.在一計算機系統中,每一循環具有誤差的機率取決於先前一個循環是否有誤差。以0表示誤差狀態,以1表示無誤差狀態,且狀態的一步轉移機率矩陣為
 遍歷性
遍歷性試說明相應齊次馬爾可夫鏈是遍歷的,並求其平穩分布:
(1)用定義解;
(2)引用遍歷性定理解。
解:
(1)因為
 遍歷性
遍歷性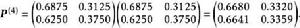 遍歷性
遍歷性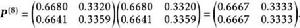 遍歷性
遍歷性 遍歷性
遍歷性由定義知,此鏈具有遍歷性,其穩態機率為
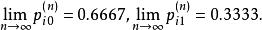 遍歷性
遍歷性(2)由定理知因為的腹元均大於0,故此鏈具有遍歷性,且其穩態機率滿足等式
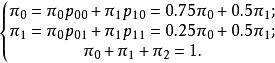 遍歷性
遍歷性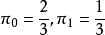 遍歷性
遍歷性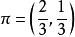 遍歷性
遍歷性解得 ,即平穩分布 。
2. 設齊次馬爾可夫鏈的一步轉移機率矩陣為
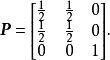 遍歷性
遍歷性證此鏈不是遍歷的。
解:因為
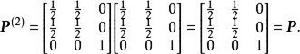 遍歷性
遍歷性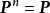 遍歷性
遍歷性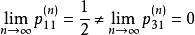 遍歷性
遍歷性故對於任意的n, ,且 ,故此鏈不是遍歷的。

