發展歷史
1819年，奧斯特發現了電流的磁作用，通過推理又導出了電流的磁化作用與電流之間的機械作用，實驗結論是:運動電荷產生磁現象。
1820年安培發現磁鐵對載流導體或載流線圈有作用力，從而得出了磁對運動電荷產生作用力的結論。至此，人們總結出磁現象與電荷的運動有密切的聯繫。
1831年法拉第經多年實驗研究，於1831年發現了磁電感應產生的條件，這一重大發現在科學技術史上具有劃時代的意義。法拉第發現了電磁感應現象，不僅揭示了電與磁相互聯繫和轉化的重要條件，而且豐富了人類對電磁現象本質的認識，開拓了電能大規模利用、傳輸的道路，導致發電機的發明和人類電氣時代的到來。法拉弟的研究方法主要是不斷依靠實驗，用實驗來檢驗他的想法，在實驗的直接影響下推動他的想法。
繼法拉第電磁感應定律之後，安培在確立電流之間機械作用定律時所用的實驗也是科學研究中最光輝的成就之一。他通過實驗得出安培定律，而我們卻看不出他的研究思想是怎樣形成的。然而這些研究方法及成果仍就是麥克斯韋電磁場理論的數學方法的基礎。
J.C.麥克斯韋提出了位移電流概念。電位移來源於電介質中的帶電粒子在電場中受到電場力的作用。這些帶電粒子雖然不能自由流動，但要發生原子尺度上的微小位移。麥克斯韋將這個名詞推廣到真空中的電場，並且認為：電位移隨時間變化也要產生磁場，因而稱一面積上電通量的時間變化率為位移電流，而電位移矢量D的時間導數（即дD/дt）為位移電流密度。它在安 培環路定律中，除傳導電流之外補充了位移電流的作用，從而總結出完整的電磁方程組，即著名的麥克斯韋方程組，描述了電磁場的分布變化規律。
1845年，關於電磁現象的三個最基本的實驗定律：庫侖定律（1785年），畢奧-薩伐爾定律（1820年），法拉第定律（1831-1845年）已被總結出來，法拉第的“電力線”和“磁力線”概念已發展成“電磁場概念”。
1855年至1865年，麥克斯韋在全面地審視了庫侖定律、畢奧—薩伐爾定律和法拉第定律的基礎上，把數學分析方法帶進了電磁學的研究領域，由此導致麥克斯韋電磁理論的誕生。
麥克斯韋電磁理論基礎的電學和磁學的經驗定律包括：靜電學的庫侖定律，涉及磁性的定律，關於電流的磁性的安培定律，法拉第電磁感應定律。麥克斯韋把這四個定律予以綜合，導出麥克斯韋方程，該方程預言：變化的電磁場以波的形式向空間傳播。 1865年麥克斯韋創立了普遍的電磁場方程組—麥克斯韋方程組,它是巨觀電磁現象的基本規律 。
1887年德國物理學家赫茲 用實驗證實了電磁波的存在。之後，人們又進行了許多實驗，不僅證明光是一種電磁波，而且發現了更多形式的電磁波，它們的本質完全相同，只是波長和頻率有很大的差別。按照波長或頻率的順序把這些電磁波排列起來，就是電磁波譜。如果把每個波段的頻率由低至高依次排列的話，它們是工頻電磁波、無線電波、微波、紅外線、可見光、紫外線、X射線及r射線。
主要方程舉例說明
即便沒有實物，占據空間的電磁場本身就具有能量、動量、角動量等傳統實物的“物質”屬性。充斥著電磁場的空間有能量、動量和角動量的存在。電磁場通過與實物的相互作用還能把能量、動量和角動量傳遞到實物中去。
自人們發現電現象、磁現象、電磁感應現象以來，對電、磁和電磁感應現象進行了深入廣泛的研究，發現了電磁之間的關係及其規律，形成了完整、系統的電磁理論。電磁理論促進了科學技術的發展，有力的推動了社會的進步。電磁理論認為：變化著的電場伴隨變化著的磁場，變化著的磁場也伴隨變化著的電場。研究過程中通過方程的形式來描述電磁場基本規律就構成了電磁場方程組 。
庫倫定律
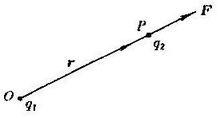庫倫定律庫侖定律描述了真空中兩個點電荷間相互作用力的規律。庫侖定律的常見表述是：真空中兩個靜止的點電荷之間的相互作用力，與它們的電荷量的乘積成正比，與它們的距離的二次方成反比，作用力的方向在它們的連線上，同名電荷相斥，異名電荷相吸。該定律由法國物理學家庫侖於1785年在《電力定律》一論文中提出。庫侖定律是電學發展史上的第一個定量規律，是電磁學和電磁場理論的基本定律之一。庫侖定律沒有解決電荷間相互作用力是如何傳遞的，甚至按照庫侖定律的內容，庫侖力不需要接觸任何媒介，也不需要時間，而是直接從一個帶電體作用到另一個帶電體上的。
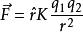電磁場方程組
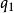電磁場方程組
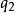電磁場方程組 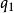電磁場方程組 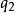電磁場方程組式中, K是比例常數，r是兩點電荷間的距離，是從 指向 的單位矢量。若 和 同號，該力是斥力，異號時為吸力。
庫侖定律是在無限大的均勻、線性、各向同性介質中總結出的實驗定律。靜電力遵從疊加原理，當有多個點電荷存在時，其中任一個點電荷受到的靜電力是其他各點電荷對其作用力的矢量疊加。對於連續分布的電荷系統（如體電荷、面電荷和線電荷），靜電力的求解不能簡單地使用庫侖定律，必須進行矢量積分。
高斯定理
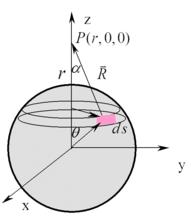
高斯定理在靜電學中，表明在閉合曲面內的電荷之和與產生的電場在該閉合曲面上的電通量積分之間的關係。高斯定律（Gauss' law）表明在閉合曲面內的電荷分布與產生的電場之間的關係。 電位移矢量在某一曲面上的面積分就是矢量通過該曲面的電通量，取積分曲面為半徑為r的球面，電通量為 ：
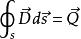電磁場方程組此通量僅取決於點電荷量q， 而與所取球面的半徑無關。 如果在封閉面內的電荷不止一個, 則利用疊加原理知, 穿出封閉面的電通量總和等於此面所包圍的總電量。
畢奧-薩伐爾定律
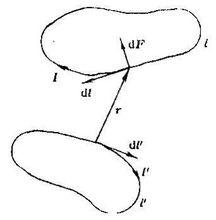
畢奧-薩伐爾定律畢奧-薩伐爾定律是由H.C.奧斯特實驗（見電流磁效應）引起的，這個實驗表明，長直載流導線對磁極的作用力是橫向力。為了揭示電流對磁極作用力的普遍定量規律，J.B.畢奧和F.薩伐爾認為電流元對磁極的作用力也應垂直於電流元與磁極構成的平面，即也是橫向力。他們通過長直和彎折載流導線對磁極作用力的實驗，得出了作用力與距離和彎折角的關係。在P.S.M.拉普拉斯的幫助下，經過適當的分析，得到了電流元對磁極作用力的規律。根據近距作用觀點，它現在被理解為電流元產生磁場的規律。
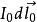電磁場方程組畢奧-薩伐爾定律適用於計算一個穩定電流所產生的磁場。這電流是連續流過一條導線的電荷，電流量不隨時間而改變，電荷不會在任意位置累積或消失。採用國際單位制，用方程表示，電流元 產生的磁感應強度為：
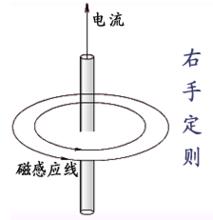右手定則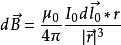
電磁場方程組
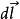電磁場方程組
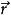電磁場方程組
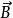電磁場方程組，，三者滿足右手螺旋關係。
積分通常圍繞閉合曲線，因為電流只能在閉合路徑周圍流動。無限長的電線（如電流SI單位定義中所使用的安培）是一個反例。要套用公式，可以任意選擇要計算磁場的空間點（r）。保持該點固定，計算電流路徑上的線積分以找出該點處的總磁場。該法的套用隱含地依賴於磁場的疊加原理，即磁場是由電線的每個無窮小部分單獨產生的場的向量和的事實。
安培環路定律
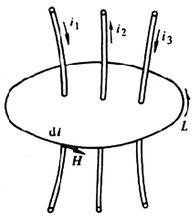安培環路定理在穩恆磁場中，磁感應強度B沿任何閉合路徑的線積分，等於這閉合路徑所包圍的各個電流的代數和乘以磁導率，這個結論稱為安培環路定理。安培環路定理可以由畢奧－薩伐爾定律導出。它反映了穩恆磁場的磁感應線和載流導線相互套連的性質。
按照安培環路定理 ，環路所包圍電流之正負應服從右手螺旋法則在恆定磁場中，磁場強度矢量沿任意閉合路徑l的環量等於其與迴路交鏈的電流之和 ，即：
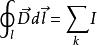電磁場方程組利用安培環路定理求磁場的前提條件：如果在某個載流導體的穩恆磁場中，可以找到一條閉合環路l，該環路上的磁感強度B大小處處相等，B的方向和環路的繞行方向也處處同向，這樣利用安培環路定理求磁感強度B的問題，就轉化為求環路長度，以及求環路所包圍的電流代數和的問題，即利用安培環路定理求磁場的適用範圍：在磁場中能否找到上述的環路，取決於該磁場分布的對稱性，而磁場分布的對稱性又來源於電流分布的對稱性。
麥克斯韋方程組
麥克斯韋方程組是電磁場方程組的基本方程組。麥克斯韋綜合了靜電學的庫侖定律，涉及磁性的定律，關於電流的磁性的安培定律，法拉第電磁感應定律四個定理導出麥克斯韋方程，創立了普遍的電磁場方程組—麥克斯韋方程組,它是巨觀電磁現象的基本規律 。
克斯韋方程組乃是由四個方程共同組成的：
高斯定律：該定律描述電場與空間中電荷分布的關係。電場線開始於正電荷，終止於負電荷。計算穿過某給定閉曲面的電場線數量，即其電通量，可以得知包含在這閉曲面內的總電荷。更詳細地說，這定律描述穿過任意閉曲面的電通量與這閉曲面內的電荷之間的關係。
高斯磁定律：該定律表明，磁單極子實際上並不存在。所以，沒有孤立磁荷，磁場線沒有初始點，也沒有終止點。磁場線會形成循環或延伸至無窮遠。換句話說，進入任何區域的磁場線，必需從那區域離開。以術語來說，通過任意閉曲面的磁通量等於零，或者，磁場是一個無源場。
法拉第感應定律：該定律描述時變磁場怎樣感應出電場。電磁感應是製造許多發電機的理論基礎。例如，一塊旋轉的條形磁鐵會產生時變磁場，這又接下來會生成電場，使得鄰近的閉合電路因而感應出電流。
麥克斯韋-安培定律：該定律闡明，磁場可以用兩種方法生成：一種是靠傳導電流（原本的安培定律），另一種是靠時變電場，或稱位移電流（麥克斯韋修正項）。
方程組形式如下所示：
1.高斯定律：該定律描述電場與空間中電荷分布的關係。電場線開始於正電荷，終止於負電荷。計算穿過某給定閉曲面的電場線數量，即其電通量，可以得知包含在這閉曲面內的總電荷。更詳細地說，這定律描述穿過任意閉曲面的電通量與這閉曲面內的電荷之間的關係。
2.高斯磁定律：該定律表明，磁單極子實際上並不存在。所以，沒有孤立磁荷，磁場線沒有初始點，也沒有終止點。磁場線會形成循環或延伸至無窮遠。換句話說，進入任何區域的磁場線，必需從那區域離開。以術語來說，通過任意閉曲面的磁通量等於零，或者，磁場是一個無源場。
3.法拉第感應定律：該定律描述時變磁場怎樣感應出電場。電磁感應是製造許多發電機的理論基礎。例如，一塊旋轉的條形磁鐵會產生時變磁場，這又接下來會生成電場，使得鄰近的閉合電路因而感應出電流。
4.麥克斯韋-安培定律：該定律闡明，磁場可以用兩種方法生成：一種是靠傳導電流（原本的安培定律），另一種是靠時變電場，或稱位移電流（麥克斯韋修正項）。
方程組形式如下所示：
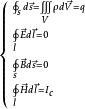電磁場方程組以上是麥克斯韋方程組積分形式，反映了空間某區域的電磁場量(D、E、B、H)和場源(電荷q、電流I)之間的關係。以自由電荷和自由電流為源頭，而不直接計算出現於電介質的束縛電荷和出現於磁化物質的束縛電流和電極化電流所給出的貢獻。由於在一般實際狀況，能夠直接控制的參數是自由電荷和自由電流，而束縛電荷、束縛電流和電極化電流是物質經過極化後產生的現象，採用這種表述會使得在介電質或磁化物質內各種物理計算更加簡易。
波動方程
波動方程或稱波方程（wave equations） 由麥克斯韋方程組導出的、描述電磁場波動特徵的一組微分方程，是一種重要的偏微分方程，主要描述自然界中的各種的波動現象，包括橫波和縱波，例如聲波、光波和水波。波動方程抽象自聲學，電磁學，和流體力學等領域。
在無源區域中充滿均勻、線性、各向同性的無耗媒質空間中，由麥克斯韋方程組，r=0，J=0可推出無源區電場波動方程
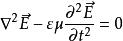電磁場方程組同理，可以推得無源區磁場波動方程為：
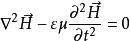電磁場方程組時變電磁場的電場場量和磁場場量在空間中是以波動形式變化的，因此稱時變電磁場為電磁波。建立波動方程的意義：通過解波動方程，可以求出空間中電場場量和磁場場量的分布情況。但需要注意的是：只有少數特殊情況可以通過直接求解波動方程求解。
意義
電磁學理論的發展在早期只是通過自然的語言描述電磁場中的一些規律。 法拉弟的研究方法主要是不斷依靠實驗，用實驗來檢驗他的想法，在實驗的直接影響下推動他的想法。由於他不是一個專業的數學家，他的研究成果沒有用嚴謹的數學形式表示出來，只是用自然的、非技術的語言把這些事實表示出來。安培在確立電流之間機械作用定律時所用的實驗也是科學研究中最光輝的成就之一。他通過實驗得出安培定律，而我們卻看不出他的研究思想是怎樣形成的。
電磁學方程組著手從數學上闡述電和磁的理論，致力於解釋法拉弟等物理學家對電磁學的研究成果。具有重要意義。 數學家的推理技巧使物理實驗家看出他所測量出來的量是由一些必然的關係聯繫起來的。物理學家的發現向數學家揭示出一些形式新穎的量，那是數學家想像不出來的。物理學家用數學形式描述自然界的規律，賦予數學符號以明確的客觀意義。
數學家對數或量的符號進行某些腦力運算，並且從簡單到複雜。這樣我們能用不同的方式來表示同一事物，這些不同方式是等價的。數學家經過長期實踐，已經成為將一種方式轉化為另一種方式的專家，能夠把令人困惑的表達轉化為另一種可以用更易理解的語言來說明其意義的表達。
物理學研究總是不斷揭示自然過程的新特徵，因此我們總是在尋求適合這些新特徵的新思想方式，重要的是仔細研究數學和物理學之間的關係。物理學研究人員觀察不同情況下發生的各種現象，並力圖推導出各種關係的規律。隨著科學的發展，人們意識到要理解事物的過程及本質，首先應明確它屬於哪一類，有多少種。這樣數量質量被認為是科學探索中有待觀察的主要特徵。而且量的範疇也侵人到質的範疇，科學研究過程成為各種量的研究過程。研究人員把注意力集中到了認為是數量的那些現象的特徵上，並尋找這些數量的內在聯繫，即物理學的研究也置於數學推理的影響之下。
數學家的推理技巧使物理實驗家看出他所測量出來的量是由一些必然的關係聯繫起來的。物理學家的發現向數學家揭示出一些形式新穎的量，那是數學家想像不出來的。物理學家用數學形式描述自然界的規律，賦予數學符號以明確的客觀意義。
