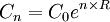連續複利收益率、年度百分率與有效年利率
連續複利收益率(Continuously compounded rate of return,CCR)
年度百分率(annual percentage rate,APR)
有效年利率(Effective Annual Rates,EAR)
T為持有期
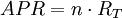 連續複利收益率
連續複利收益率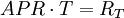 連續複利收益率
連續複利收益率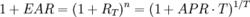 連續複利收益率
連續複利收益率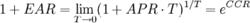 連續複利收益率
連續複利收益率短期投資利率常用APR來表示,一年有n=1/T期,每期利率為RT ,則
CCR = ln(1 + EAR)
參考文獻
1 孫伍琴,王朝暉,熊樂星.證券投資學.上海市:立信會計出版社,2008.