連續介質波動理論
正文
研究波在連續介質中傳播的一般理論和計算方法。按照理性力學的觀點，波可定義為任意一個張量場＝(x,t)隨時間t在空間的傳播,其中x是質點的空間位置。它具有雙重涵義：一是指需要研究奇異面σ(t)在空間的傳播與的間斷量（又稱跳變數）之間的相互關係,以便弄清波動的局部性質；二是指需要研究在σ(t)兩側σ 的空間分布隨時間的變化，以便弄清波動的總體性質。60年代以前，幾乎沒人研究過有限變形條件下非線性介質中的波動理論。理性力學的發展，使人們對物質的本構關係有了比較深入和系統的認識，而運用在此同時發展起來的一種嚴格的分析方法也有利於研究在各種介質中，尤其是在熱彈性介質和減退記憶介質中波的形成、發展、相互轉化和相互作用的規律，從而把古典彈性力學和流體力學研究波動問題的方法向前推進一步。於是波動理論就成為理性力學的一個重要分支。這個方法的理論基礎就是奇異面理論，即利用奇異面上的相容性條件、波陣面兩側的守恆方程和具體物質的本構關係進行嚴格數學運算，從而得出波的傳播特性。奇異面σ(t)和張量值函式及其各階導數的間斷之間的相容性關係包括幾何學相容性條件、運動學相容性條件和動力學相容性條件，即：
①幾何相容性條件 系指對空間坐標導數的間斷【д/дxi】、沿σ(t)法嚮導數的間斷和σ（t）幾何性質相互連繫的普遍關係式，這裡不涉及曲面的運動特性。【 】表示括弧內的量在σ(t) 的“＋”側和“－”側兩值之差。J.阿達瑪於1903年給出一個著名的引理,即“對奇異面σ(t)，若д/дxi存在間斷，即【д/дxi】厵0，但本身連續，則間斷矢量【д/дxi】必和σ(t)的法矢量n平行”。這一引理常被稱為阿達瑪引理。後來,隨著理性力學的發展，T.Y.托馬斯、C.特魯斯德爾等人給出了更加一般的幾何相容性條件，其中並不要求沿σ(t)保持連續。在得到一階導數間斷的相容性條件的基礎上，通過疊代法可求得關於的高階導數間斷的相容性條件。在研究固體在有限變形下的波動問題時，常常採用物質坐標，因此需要給出在該坐標系下的相容性條件。
②運動學相容性條件 表示間斷【】沿σ(t)的變化率、σ(t)在空間的法向運動速度un和間斷【д/дt】之間的相互關係。若引用δ ──時間導數的概念，則運動學相容性條件可表示為：
δ【】/δt=【д/дt】+un【niд/дxi】
③動力學相容性條件 表示跨越σ(t)時，物體的運動必須遵循質量守恆定律、動量和動量矩平衡定律、能量守恆定律以及熵不等式。
由於這些相容性條件並不涉及物質本構方程的具體形式，因而它們對所有物質都是普遍適用的。正因為如此，奇異面上的相容性條件才成為研究各種介質中波動特性的有力工具。
奇異面σ(t)按其對φ的間斷性質可分成兩大類:一類是強間斷,即【】厵0;另一類是弱間斷,即沿σ(t)連續，但它的空間或時間導數存在間斷。激波是關於運動(把視為變形介質的運動)的一階奇異面;而加速度波則是關於運動的二階奇異面。
目前，對非線性介質中激波問題的研究採用兩種分析方法:一是解析方法,包括簡單波理論、特徵理論、半逆法和無窮級數法，用這些方法可以獲得少數問題的精確解；二是構成各類物質關於激波幅度隨波傳播時的增、衰方程，討論激波傳播的局部性質。用這種方法證明在高分子聚合物、有機玻璃一類粘彈性物質中有兩種因素控制著波的傳播：非線性彈性性質使波幅增加，而粘性則使波幅衰減，在某種組合條件下，能形成穩定的激波。這一點已為平板撞擊試驗所證實。關於加速度波問題的研究在非線性介質波動理論中占有重要地位。這是因為非線性介質中的加速度波具有根本不同於線性介質中的若干特性。加速度波的幅值矢量a和波的局部傳播速度U滿足下列關係式：
，
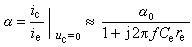δа/δt＝-μ(t)а+β(t)а2，
式中,係數μ(t）由材料的性質、波陣面上的狀態和形狀決定，而係數β(t)只和介質的瞬態彈性反應有關。當波陣面處於均勻變形狀態時，係數μ和β為常數。加速度波的這個性質十分重要，它預示在介質中存在一個臨界的加速度波的初始幅值а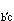
。當а0＞а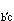時,波幅隨波的傳播而增加，因而經過有限時間，加速度波可以發展成激波；當а0＜а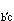時，波幅是衰減的；當а0=а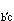時，加速度波在傳播過程中保持穩定。這一點和線性介質顯然不同，並已為實驗所證實。 近二十年來，不少學者利用理性力學的奇異面理論開展了各種不同介質中激波和加速度波傳播性質的系統研究，其中包括彈性固體、熱彈性固體、非線性粘彈性體、剛塑性體、電磁介質、化學反應介質、微極彈性介質、複合材料等方面，都獲得了很大的進展。但這種方法只能定性地討論無限域中非線性波動傳播的局部性質，除少數簡單情況可以得到解析解外，要了解波動的總體性質仍需藉助數值計算。
參考書目
C.Truesdell and R.Toupin, The Classical Field Theories,Handbuch der Physik, Bd.Ⅲ/1, Springer-Verlag,Berlin,Gttingen,Heidelberg,1960.
C.Truesdell and W.Noll, The Non-linear FieldTheoriesof Mechanics, Handbuch der Physik, Bd. Ⅲ/3,Springer-Verlag,Berlin,Heidelberg,New York,1965.
A.C.Eringen and E.S.Suhubi, Elastodynamics,Vol.1,Academic Press,New York,1974.
