定義
所謂逐差法，就是把測量數據中的因變數進行逐項相減或按順序分為兩組進行對應項相減，然後將所得差值作為因變數的多次測量值進行數據處理的方法。
逐差法套用實例
在高中物理“求勻變速直線運動物體的加速度”實驗中分析紙帶。
運用公式△X=at^2;
X-X=X-X=X-X
當時間間隔T相等時，假設測得 X,X,X,X 四段距離，那么加速度
a=【(X-X)+(X-X)】/2×2T
逐差法不確定度
例如牛頓環實驗
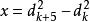逐差法其中k=1,2,3,4,5.共測10個環的直徑，d1<d2<……<d10
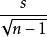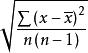逐差法
逐差法x的a類不確定度為=，其中s為樣本方差
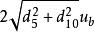逐差法x的b類不確定度為（這裡取d5d10，因為這樣計算得到的不確定度最大，比較保守）
牛頓環實驗的b類不確定度要用 配對的數據計算，本例中不能用d10d9計算b類不確定度，因為逐差法中d10和d5才是配對的。
加速度逐差法
a類不確定度算法類似
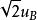逐差法b類不確定度為，和牛頓環實驗完全不同。
線性回歸
要想更精確地求出擬合方程，可以用線性回歸的方法。
逐差法適合手工計算，線性回歸一般藉助excel或統計軟體。
輾轉相除
輾轉相除法有時也稱作逐差法。
逐差法（輾轉相除法、更相減損術）求最大公約數：
兩個正整數，以其中較大數減去較小數，並以差值取代原較大數，重複步驟直至所剩兩數值相等，即為所求兩數的最大公約數。
例如：
259，111 ==>259-111=148
148，111 ==>148-111=37
111，37 ==>111- 37=74
74 ，37 ==> 74- 37=37
37 ，37 ==> 259與111的最大公約數為37
