形成和表示
假如使曲線ABC（母線）繞一軸線O-O（導線）旋轉，所得的曲面叫做迴轉面（如圖a）。
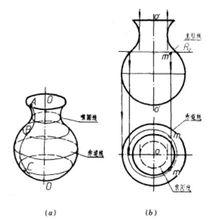迴轉面的形成與畫法在旋轉時，曲線上每一點所形成的圓叫做緯線。在緯線中有這樣兩種圓：當它比兩側相鄰的緯線都大時，稱為赤道線；比兩側的相鄰緯線都小時，稱為喉圓線。
通過軸線O-O的平面與迴轉面的交線，叫做經線。與投影面平行的經線叫做主經線。
在投影圖上表示迴轉面時，常常使它的軸線垂直於某一投影面（如上圖b）。在作圖時應當先畫出作為導線的軸線的投影（通常用點劃線表示），然後在各投影上畫出曲面的輪廓線。迴轉面的正面投影輪廓線是主經線的正面投影，它的水平投影輪廓線是赤道線和喉圓線的水平投影，此外，由於迴轉面是對稱的，按照習慣，在水平投影中還應該畫出對稱線（用點劃線表示）。
一般性質
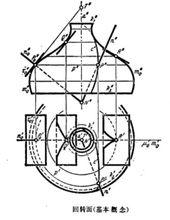迴轉面一條曲線c繞一條軸線a旋轉（如右圖，其中c不能是一個圓周，因為它在旋轉後將轉到原位置。），由c構成的曲面Φ叫做迴轉面（旋轉面）。在繞a轉時，c上每—點P形成Φ的一個緯圓p。Φ上與所有緯圓相交的任一其它曲線，繞a旋轉時產生同一個迴轉面。一條位於經過a並平行於正面投影面的平面μ上的那種曲線，為Φ的“主子午線”m；P繞a旋轉到μ上時，得出m上P點，同樣地可在m上得出與P對稱於a的點。Φ與一個通過a的平面μ的相交線m，叫做Φ的一條子午線或輪廓線。m是由對稱於a的兩條“半子午線”組成。因為每個緯圓對稱於μ，故Φ對稱於μ。Φ上所有子午線是全同的，因而每條子午線的正面投影m''透視仿射對應於m''。
Φ在P點的切平面τ包含有P處p和m的切線，於是τ反映為直線τ''。繞a旋轉時，τ變成p上另一點的切平面。這些切平麵包絡著一個正圓錐面（頂點T，軸a）。這個正圓錐面也由P處子午切線繞a旋轉來形成。在p上各點的曲面法線n形成另一個正圓錐面（頂點N，軸a）。以N為中心，經過P的球面，沿著p切於Φ。
如果p是一條赤道或一個喉圓（最大及最小的緯圓），則τ''∥a''，切平麵包絡一個正圓柱面，p的直徑是曲面法線。如果τ''⊥a''，則p稱為Φ的平圓；曲面法線組成通過p的正圓柱面，p的平面沿著p切於Φ。每條赤道或每個喉圓屬於Φ的第一外形線。m''和平圓的圖象屬於Φ的第二外形線。邊圓，如圖275中k和k，可以計入第一和第二外形線。
橢圓型的及雙曲型的曲麵點，出現於迴轉面上那種地方，即子午線的凹邊及凸邊朝向迴轉軸的地方（如上圖中P及Q）。子午線的反曲點和平圓上的點是Φ的拋物點（如上圖中R）。
下圖表示一個迴轉面在工程上的一般表示法（左面為子午斷面，右邊為視圖，水平投影常常省略）。
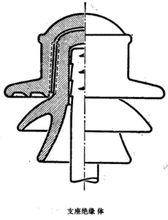支座絕緣體常見的迴轉面
圓柱面
1.圓柱面的形成
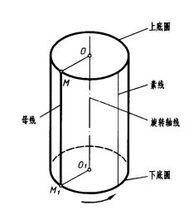圓柱面的形成圓柱面是由直母線繞與它平行的軸線旋轉360°而形成的曲面，圓柱面上所有的素線均平行於軸線，且到軸線的距離相等，如圖所示。母線的兩端點M和M旋轉形成的上、下兩個圓周稱為上、下底圓。當軸線垂直於上下底圓平面時的圓柱面稱為正圓柱面，簡稱圓柱面。
2.圓柱面的投影
當圓柱面的軸線垂直於水平投影面時，其三面投影如圖所示，圓柱面所有的素線都垂直於水平投影面，其水平投影積聚為一圓周。值得注意的是畫圖時必須將相互垂直的直徑ac和bd用單點長畫線畫出，兩單點長畫線的交點表示圓心的位置，它們與圓周的交點是圓柱面的正面轉向輪廓線和側面轉向輪廓線的水平投影。圓柱面的正面投影和側面投影都為矩形，矩形的上、下兩水平線段為上底圓和下底圓的積聚性投影，鉛垂的單點長畫線為軸線的投影。在正面投影中，a'a'和c'c'輪廓線為圓柱面最左素線AA和最右素線CC的投影，稱為正面轉向輪廓線，同時也是前、後兩個半圓柱面可見與不可見部分的分界線，因為圓柱面是光滑的曲面，所以這兩條轉向輪廓線的側面投影不必畫出。在側面投影中，b"b"和d"d"輪廓線為圓柱面最前素線BB和最後素線DD的投影，稱為側面轉向輪廓線，同時也是左、右兩個半圓柱面在側面投影中可見與不可見部分的分界線。同理這兩條側面轉向輪廓線的正面投影也不必畫出。
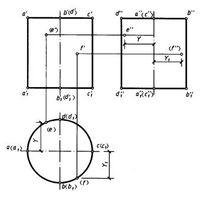圓柱面的投影及面上取點3.圓柱面上取點
圓柱面上取點與平面上取點原理相同，可過點在圓柱面上作一輔助線來求解。為作圖方便，根據圓柱面的投影特性可利用素線作為輔助線。
圓錐面
1.圓錐面的形成
圓錐面是由直母線繞與它相交的軸線旋轉360°形成的曲面。如圖所示的圓錐面足由直母線SM繞與其相交於點S的軸線OO旋轉360°形成的。S稱為圓錐的錐頂，母線的端點M旋轉形成的一個圓周稱為下底圓。圓錐面上通過錐頂S的任一直線稱為圓錐面的素線。
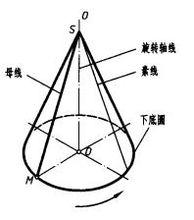圓錐面的形成2.圓錐面的投影
當圓錐面的軸線垂直於水平投影面時，其三面投影如圖所示。水平投影為一圓形，圓形為圓錐面的水平投影，圓形的圓周為圓錐面下底圓的水平投影；圓錐面的正面投影和側面投影均為等腰三角形，在正面投影中，等腰三角形的兩腰為圓錐面的正面轉向輪廓線（最左素線和最右素線）的投影；在側面投影中，等腰三角形的兩腰為圓錐面的側面轉向輪廓線（最前素線和最後素線）的投影。
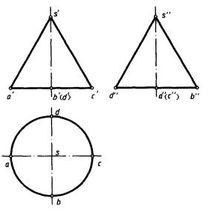圓錐面的投影圓錐面上兩條正面轉向輪廓線和兩條側面轉向輪廓線，在正面投影和側面投影中分別構成圓錐面的投影輪廓線，如上圖中的SA和SC，SB和SD。圓錐面投影的可見性為：水平投影中整個圓錐面都是可見的；正面投影中圓錐面的前半部分可見，後半部分不可見；側面投影中，圓錐面的左半部分可見，右半部分不可見。值得注意的是圓錐面的三面投影均無積聚性。儘管圓錐面的軸線垂直於某投影面，在該投影面上的投影也是圓，但此圓並非圓錐面的積聚投影。
3.圓錐面上取點
圓錐面的三面投影均無積聚性，在其面上取點就不能採用在圓柱面上取點的方法來求解，而需根據圓錐面的投影性質，通過作過錐頂的素線或作過定點的緯圓等方法來求解。
球面
1.球面的形成
球面是由圓母線繞其自身的一根直徑為軸旋轉180°而形成的曲面，如圖a所示。球面也可看做半圓母線繞其自身的直徑為軸旋轉360°而形成。
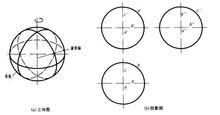球面的形成與投影2.球面的投影
球面的三面投影均為一直徑等於球直徑的圓，如圖b所示，分別用a'，b，c''表示。a'，b，c''三個圓分別是球面的正面轉向輪廓線、水平轉向輪廓線和側面轉向輪廓線的投影，也即分別是球面的前後半球面、上下半球面和左右半球面的分界線的投影。必須注意的是三面投影中都應畫出圓的中心線。
3.球面上取點
因為球面是非直紋曲面，其母線是曲線而不是直線，所以球面上點的投影只能利用緯圓法求出。為作圖方便，應選擇平行於某一投影面的圓周作為輔助圓。
圓環面
1.圓環面的形成
圓環面是由圓母線繞與它共面的圓外一直線為軸旋轉360°而形成的曲面。母線上任意一點運動的軌跡均為圓周，圓周所在的平面垂直於迴轉軸線。最大和最小的圓周分別稱為赤道圓和頸圓。
2.圓環面的投影
當圓環面的軸線垂直於水平投影面時，其三面投影如圖所示，其水平投影為兩個同心圓，分別是圓環面的赤道圓和頸圓的投影；圓心為圓環的迴轉軸線的積聚投影；單點長畫線圓為母線圓心運動軌跡的水平投影。正面投影兩端的兩個圓分別是圓環面最左素線圓和最右素線圓的投影。側面投影兩端的兩個圓分別是圓環面最前素線圓和最後素線圓的投影。正面和側面投影中兩素線圓的上、下兩水平公切線則是母線圓的最高和最低點的運動軌跡的投影。
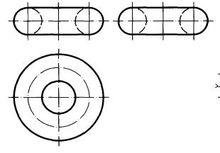圓環面的投影3.圓環面上取點
因為圓環面的母線是曲線，所以圓環面上點的投影只能利用緯圓法求出。
單葉雙曲迴轉面
1.單葉雙曲迴轉面的形成
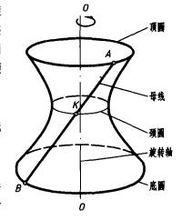單葉雙曲迴轉面的形成單葉雙曲迴轉面是由直母線AB繞與它交叉的軸線OO旋轉360°而形成的曲面，如圖所示。母線上各點的運動軌跡均為垂直於OO的緯圓，兩端點A和B旋轉形成該曲面的頂圓和底圓，母線上距軸線最近的點K旋轉形成該曲面的頸圓，頸圓的半徑為兩交叉直線的公垂線的長度。
2.單葉雙曲迴轉面的投影
單葉雙曲迴轉面的母線為直線，因此求其投影既可用素線法也可用緯圓法。
