基本內容
辛欽大數定律的基本內容是：設X1,X2,⋯是獨立同分布的隨機變數序列，且它們的期望值存在，記為E(Xi)=μ(i=1,2,⋯)，則對於任意的ɛ>0，有
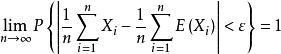辛欽大數定律辛欽大數定律從理論上指出：用算術平均值來近似實際真值是合理的，而在數理統計中，用 算術平均值來估計數學期望就是根據此定律，這一定律使算術平均值的法則有了理論依據 。
舉例說明
例如，當我們要測量某個物理量a時，在不變的條件下重複測量n次，得到的結果為X1,X2,⋯,Xn，此時我們取算術平均值
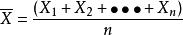辛欽大數定律
辛欽大數定律作為a的近似值，而且隨著n的增大， 與a之間的誤差會越來越小。
辛欽大數定律是近代保險業賴以建立的數理基礎。保險公司正是利用在個別情形下存在的不確定性將在大數中消失的這種規則性，來分析承保標的發生損失的相對穩定性。按照大數法則，保險公司承保的每類標的數目必須足夠大，否則，缺少一定的數量基礎，就不能產生所需要的數量規律。但是，任何一家保險公司都有它的局限性，即承保的具有同一風險性質的單位是有限的，這就需要通過再保險來擴大風險單位及風險分散面 。
辛欽大數定律的特殊情況
伯努利大數定律的基本內容是：設μn為n重伯努利實驗中事件A發生的次數，p為A在每次實驗中發生的機率，則對任意給定的實數ε>0，有
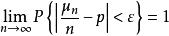辛欽大數定律顯然，伯努利大數定律是辛欽大數定律的特殊情況，辛欽大數定律在實際中套用很廣泛。
注意事項
(1)辛欽大數定律並不要求隨機變數序列X1,X2,⋯的方差存在；
(2)當Xi為服從0-1分布的隨機變數時，辛欽大數定律就是伯努利大數定律，故 伯努利大數定律是辛欽伯努利大數定律的一個特例。
