軸的基本理論

軸的基本理論

正文

以扭轉為主要變形的直桿稱為軸，如機械中的傳動軸，而在土木建築工程中習慣上稱為受扭構件。扭轉變形的特點是桿的任意兩個橫截面，繞桿的軸線發生相對轉動，如圖1。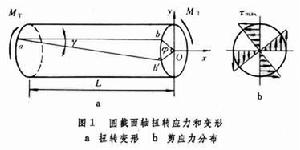

軸的基本理論

圓截面軸的扭轉　用材料力學的方法求解其應力和變形時，採用了平面假設，即認為圓軸的橫截面在軸受扭時保持為平面，且半徑仍為直線。由此得知，當軸線上彈性範圍工作時，橫截面上任一點處的剪應力 τ與該點離圓心O的距離 ρ成正比，其方向垂直於半徑,在截面周界上的各點處剪應力達到最大值。圓軸橫截面上剪應力的計算公式為

τ＝MTρ/Ip

式中MT為橫截面上的扭矩,可由截面法求得；Ip為截面的極慣性矩，對於直徑為D的實心圓截面Ip=πD4/32，對於外直徑為D,內直徑為d的空心圓截面Ip=π(D4-d4)/32。如果在長度L的區間內,扭矩MT為常量,截面尺寸不變且材料亦相同,則該區間之兩個任意橫截面的相對扭轉角為
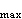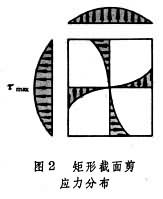
嗞＝MTL/GIp式中G為材料的剪下彈性模量；嗞的單位為弧度。在求得圓軸受扭時的應力和變形後，即可進行軸的強度和剛度計算。強度條件要求軸的橫截面上的最大剪應力，不超過材料的容許剪應力 【τ】；剛度條件要求軸的單位長度的最大扭轉角θ不超過允許的最大單位扭轉角【θ】。
非圓截面桿的扭轉　橫截面要發生翹曲(凹凸)，平面假設不適用，故此類桿件橫截面上剪應力的分布規律與圓截面軸亦不同,如圖2。其應力和變形都不能用對於圓軸扭轉的應力和變形公式計算，需要用彈性力學或實驗方法分析。

軸的基本理論

配圖

相關連線