定義
設X是非空集合,對於X中任意的兩個元素x與y,按某一法則都對應唯一的實數d(x,y),而且滿足下述三條公理:
(1)(非負性)d(x,y)≥0,[d(x,y)=0,若且唯若x=y];
(2)(對稱性)d(x,y)=d(y,x);
(3)(三角不等式)對於任意的x,y,z∈X,恆有d(x,y)≤d(x,z)+d(z,y)。
則稱d(x,y)為x與y的 距離,並稱X是以d為距離的 距離空間,記作(X,d)。通常,在距離已被定義的情況下,(X,d)可以簡單地將X中的元素稱為X中的點 。
點集
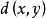 距離空間
距離空間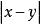 距離空間
距離空間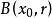 距離空間
距離空間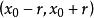 距離空間
距離空間這裡用抽象的距離 代替R中的絕對值 ,用開球 代替R中的對稱開區間 。
設(X,d)為距離空間,則可依次定義概念 :
開球
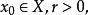 距離空間
距離空間設 稱X中的點集
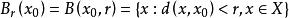 距離空間
距離空間 距離空間
距離空間 距離空間
距離空間 距離空間
距離空間 距離空間
距離空間是以 為中心,以 為半徑的 開球;又稱為 的 鄰域。
閉球
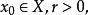 距離空間
距離空間設 稱
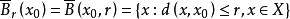 距離空間
距離空間 距離空間
距離空間 距離空間
距離空間是以 為中心,以 為半徑的 閉球。
球面
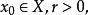 距離空間
距離空間設 稱
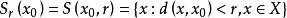 距離空間
距離空間 距離空間
距離空間 距離空間
距離空間是以 點為中心,以 為半徑的 球面。
內點
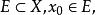 距離空間
距離空間 距離空間
距離空間 距離空間
距離空間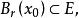 距離空間
距離空間 距離空間
距離空間設 若存在 的 鄰域 則稱點 為E的 內點,E的內點全體稱為E的 內部記為E。
開集
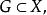 距離空間
距離空間設 若G中每一點都是其內點,則稱G為 開集。
閉集
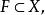 距離空間
距離空間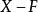 距離空間
距離空間設 若 為開集,則稱F為 閉集。
鄰域
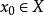 距離空間
距離空間 距離空間
距離空間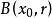 距離空間
距離空間 距離空間
距離空間包含 的任一開集均稱為 的一個鄰域,特別稱 是 的 球形鄰域,有時也簡稱 鄰域。
聚點
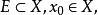 距離空間
距離空間 距離空間
距離空間 距離空間
距離空間 距離空間
距離空間 距離空間
距離空間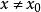 距離空間
距離空間設 若 的每一個鄰域中均含有E的無窮多個點,則稱 為E的 聚點或 極限點,E的聚點可以在E中也可不在E中, 為E的聚點可等價定義為: 的每個鄰域中含有E的點x,但 。
導集
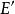 距離空間
距離空間E的聚點的全體稱為E的 導集,記為。
閉包
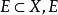 距離空間
距離空間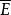 距離空間
距離空間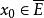 距離空間
距離空間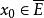 距離空間
距離空間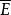 距離空間
距離空間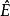 距離空間
距離空間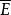 距離空間
距離空間設 的閉包 定義為 中的點又稱為E的 接觸點。可以知道 的充要條件是 因此E的閉包 又可定義為與E的距離為0的一切點的全體,E的 聚點( 極限點)必是E的 接觸點,反之則不然。
孤立點
、邊界、有界集、直徑
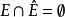 距離空間
距離空間若用 不含在E中的E的聚點集合,則有
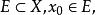 距離空間
距離空間 距離空間
距離空間(其中 ).
 距離空間
距離空間 距離空間
距離空間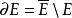 距離空間
距離空間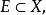 距離空間
距離空間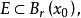 距離空間
距離空間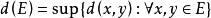 距離空間
距離空間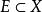 距離空間
距離空間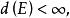 距離空間
距離空間設 若 的某一鄰域中沒有除 以外的E的其他點,則稱 為E的 孤立點。稱 為E的 邊界;設 若則稱E為 有界集;稱 為E的 直徑,如果 的直徑 ,則E是 有界集 。

